题目内容
20.关于x的方程x2+2mx+m2+m-5=0有整数根,且m为正整数,则m的值为1或5.分析 首先求得根的判别式△=20-4m≥0,得出m≤5;利用公式法解方程得到x1=-m+$\sqrt{5-m}$,x2=-m-$\sqrt{5-m}$,然后利用整数的整除性与二次根式的性质确定正整数m的值.
解答 解:∵关于x的方程x2+2mx+m2+m-5=0有整数根,
∴△=20-4m≥0,解得m≤5,
∴x=$\frac{-2m±2\sqrt{5-m}}{2}$,
∴x1=-m+$\sqrt{5-m}$,x2=-m-$\sqrt{5-m}$,
则$\sqrt{5-m}$为整数,且m为正整数,
∴m=1或m=5.
故答案为:1或5.
点评 此题考查根的判别式的知识,解答本题的关键是掌握根的判别式与根的个数的关系.

练习册系列答案
相关题目
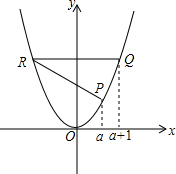 已知P,Q,R是抛物线y=x2上不同的三点,设P,Q的横坐标分别为a,a+1(a>0),R与Q是关于y轴对称的两点.
已知P,Q,R是抛物线y=x2上不同的三点,设P,Q的横坐标分别为a,a+1(a>0),R与Q是关于y轴对称的两点. 如图,在△ABC中,BC边上的高为AD,AC边上的高为BE,BC=8,AD=5,AC=6,求BE的长.
如图,在△ABC中,BC边上的高为AD,AC边上的高为BE,BC=8,AD=5,AC=6,求BE的长.