题目内容
4.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x-y=3a+1}\\{x+2y=4-2a}\end{array}\right.$的解x、y都是正数,求a的取值范围.分析 先解二元一次方程组,然后根据x、y都是正数,从而可以确定a的取值范围.
解答 解:$\left\{\begin{array}{l}{2x-y=3a+1}&{①}\\{x+2y=4-2a}&{②}\end{array}\right.$
①×2+②,得
5x=4a+6
解得,x=$\frac{4a+6}{5}$,
将x=$\frac{4a+6}{5}$代入①,得
y=$\frac{-7a+7}{5}$
∵x、y都是正数,
∴$\left\{\begin{array}{l}{\frac{4a+6}{5}>0}\\{\frac{-7a+7}{5}>0}\end{array}\right.$
解得$-\frac{3}{2}<a<1$,
即a的取值范围是$-\frac{3}{2}<a<1$.
点评 本题考查二元一次方程组的解,解题的关键是会二元一次方程组的解法,可以将二元一次方程组解转化为不等式的关系.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
16.下面每个选项中给出了某个变化过程中的两个变量x和y,其中y不是x的函数的选项是( )
| A. | y:正方形的面积;x:这个正方形的周长 | |
| B. | y:某学生的身高;x:这个学生的年龄 | |
| C. | y:圆的面积;x:这个圆的直径 | |
| D. | y:一个数的平方根;x:这个正数 |
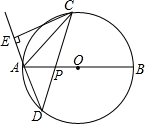 如图,在半径为r的⊙O中,直径AB与弦CD相交于点P,CE⊥DA交DA的延长线与E,连接AC.
如图,在半径为r的⊙O中,直径AB与弦CD相交于点P,CE⊥DA交DA的延长线与E,连接AC. 如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.
如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍. 如图所示,把一个等腰三角形纸片按底边上的高线剪开成为两个三角形纸片,现在要用这两个三角形纸片拼合成与原等腰三角形不同的三角形或四边形,并且要求拼合成的图形是轴对称图形,则这样的图形有3个.
如图所示,把一个等腰三角形纸片按底边上的高线剪开成为两个三角形纸片,现在要用这两个三角形纸片拼合成与原等腰三角形不同的三角形或四边形,并且要求拼合成的图形是轴对称图形,则这样的图形有3个.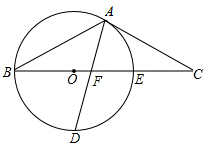 如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.
如图,以△ABC的BC边上一点O为圆心的圆经过A,B两点,且AC是切线,⊙O与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F.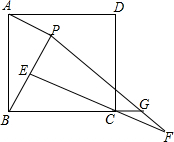 如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.
如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.