题目内容
15.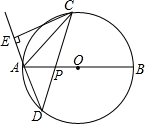 如图,在半径为r的⊙O中,直径AB与弦CD相交于点P,CE⊥DA交DA的延长线与E,连接AC.
如图,在半径为r的⊙O中,直径AB与弦CD相交于点P,CE⊥DA交DA的延长线与E,连接AC.(1)若$\widehat{AD}$的长为$\frac{2}{9}$πr,求∠ACD的度数;
(2)若$\widehat{AC}$=$\widehat{BC}$,tan∠DAB=3.CE+AE=3,求r的值.
分析 (1)连接OD,根据已知条件和圆的周长公式即可得到结论;
(2)连接BD,根据已知条件得到∠ADC=45°,根据等腰直角三角形的性质得到ED=CE,根据勾股定理即可得到结论.
解答 解:(1)连接OD,
∵$\widehat{AD}$的长为$\frac{2}{9}$πr,⊙O的周长=2πr,
∴∠AOD=360°×$\frac{\frac{2}{9}πr}{2πr}$=40°;
∴∠ACD=20°.
(2)连接BD,
∵$\widehat{AC}$=$\widehat{BC}$,
∵∠ADC=45°,
∵CE⊥DA,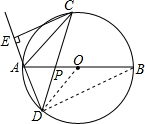
∴∠AEC=90°,
∴DE=CE,
∵CE+AE=3,
∴设AE=x,CE=3-x,
∴AD=3-2x,
∴AC2=x2+(3-x)2,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AB2=2AC2=2[x2+(3-x)2],
∵tan∠DAB=3,
∴BD=3AD,
∴AB2=AD2+BD2,
即2[x2+(3-x)2]=(3-2x)2+[3(3-2x)]2,
∴x=1,x=2(不合题意,舍去),
∴AB=$\sqrt{10}$,
∴r=$\frac{\sqrt{10}}{2}$.
点评 本题考查了弧长的计算,勾股定理,等腰直角三角形的性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.
其中正确的是( )
 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.
其中正确的是( )
| A. | ②③④ | B. | ②④ | C. | ①③④ | D. | ②③ |
6.|-9|的相反数是( )
| A. | -9 | B. | 9 | C. | 3 | D. | 没有 |
11.下列各数中,最小的数是( )
| A. | 5 | B. | -$\sqrt{3}$ | C. | π | D. | -1 |