题目内容
12. 如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.
如图,在正方形ABCD中,线段EF,GH分别与正方形两边平行,且EF,GF相交于点M,连接AF,AH,AE的长为m,AG的长为n,矩形CFMH的面积是矩形AEMG的面积的2倍.(1)求点H,F之间的距离.(用m,n表示)
(2)猜出∠FAH的度数,并说明你的理由.
分析 (1)设正方形边长为a,AG=m,GP=n,则HC=a-n,CF=a-m,根据矩形CFMH的面积是矩形AEMG的面积的2倍,得到a2-(m+n)a=mn,再根据FH2=CH2+CF2,计算即可解决问题.
(2)结论:∠FAH=45°.连结FH,延长CB到N,使BN=DF,连结AN,先证明△ABN≌△ADF,推出∠FAN=90°,再证明△ANF≌△AFH即可解决问题.
解答 (1)解:设正方形边长为a,AG=m,GP=n,则HC=a-n,CF=a-m,
∵矩形CFMH的面积是矩形AEMG的面积的2倍
∴a2-(m+n)a+mn=2mn,
∴a2-(m+n)a=mn,
在直角三角形FCH中,∵FH2=CH2+CF2,
∴FH2=(a-n)2+(a-m)2=2a2-2(m+n)a+m2+n2=(m+n)2,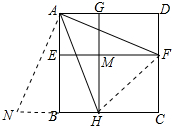
∵FH>0,
∴FH=m+n.
(2)结论:∠FAH=45°.
证明:如图,连结FH,延长CB到N,使BN=DF,连结AN,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABH=∠ABN=90°,
在△ABN和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABN=∠D}\\{BN=DF}\end{array}\right.$,
∴△ABN≌△ADF,
∴AN=AF,∠NAB=∠FAD,
∴∠NAF=∠NAB+∠BAF=∠BAF+∠FAD=90°,
∵NH=m+n,FH=m+n,
∴FH=NH,
在△AHF和△AHN中,
$\left\{\begin{array}{l}{AH=AH}\\{AF=AN}\\{HF=HN}\end{array}\right.$,
∴△ANF≌△AFH,
∴∠HAF=∠HAN,
∵∠FAN=90°,
∴∠FAH=$\frac{1}{2}$∠FAN=45°.
点评 本题考查正方形的性质、矩形的性质、全等三角形的判定和性质勾股定理等知识,解题的关键是添加辅助线构造全等三角形,学会常用辅助线的添加方法,属于中考常考题型.

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案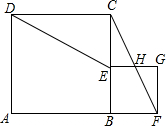 如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.
如图,点B在线段AF上,分别以AB、BF为边在线段AF的同侧作正方形ABCD和正方形BFGE,连接CF和DE,CF交EG于H.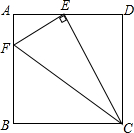 如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.
如图,已知E是矩形ABCD边AD的中点,F是AB上一点,EF⊥CE,若AB:BC=$\sqrt{3}$:2,同图中(有4个三角形)相似三角形有3对.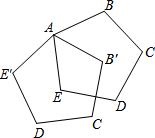 如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.
如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.