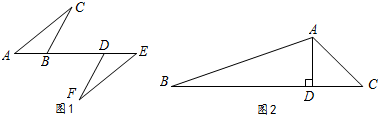题目内容
20.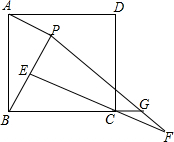 如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.
如图,P是矩形ABCD内一点,AP⊥BP于点E,CE⊥BP于点E,BP=EC.(1)请判断四边形ABCD是否是正方形?若是,写出证明过程:若不是,说明理由;
(2)延长EC到点F,使CF=BE,连接PF交BC的延长线于点G,求∠BGP的度数.
分析 (1)由四边形ABCD为矩形可得∠ABC=90°,易得∠ABP+∠PBC=90°,由AP⊥BP,可得∠ABP+∠PAB=90°,易得∠PBC=∠PAB,由AAS定理可得△ABP≌△BCE,由全等三角形的性质可得AB=BC,易得结论;
(2)连接AC,由△ABP≌△BCE易得AP=BE,又CF=BE,可得AP=CF,易得四边形ACGP是平行四边形,可得∠ACB=∠BGP,由四边形ABCD是正方形,AC是对角线,可得∠ACB=∠BGP=45°.
解答 解:(1)四边形ABCD为正方形.
∵四边形ABCD是矩形,
∴∠ABC=90°,
即∠ABP+∠PBC=90°,
∵AP⊥BP,
∴∠ABP+∠PAB=90°,
∴∠PBC=∠PAB,
∵CE⊥BP,
∴∠APB=∠BEC=90°,
在△ABP与△BCE中,
$\left\{\begin{array}{l}{∠BAP=∠CBE}\\{∠APB=∠BEC}\\{PB=EC}\end{array}\right.$,
∴△ABP≌△BCE,
∴AB=BC,
∴矩形ABCD为正方形;
(2)连接AC,
∵△ABP≌△BCE,
∴AP=BE,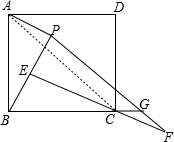
∵BE=CF,
∴AP=CF,
∵AP⊥BP,CE⊥BP,
∴AP∥CF,
∴四边形ACGP是平行四边形,
∴AC∥PF,
∴∠ACB=∠BGP,
∵四边形ABCD是正方形,AC是对角线,
∴∠ACB=45°,
∴∠BGP=45°.
点评 本题主要考查了全等三角形的判定及性质,平行四边形的性质和正方形的性质及判定,综合利用各定理是解答此题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.下列各数中,最小的数是( )
| A. | 5 | B. | -$\sqrt{3}$ | C. | π | D. | -1 |
15.下列事件是不确定事件的是( )
| A. | 抛出的石块会下落 | |
| B. | 当室外温度低于-3℃时,将一碗清水放到室外,水会结冰 | |
| C. | 任意买一张电影票,座位号是奇数 | |
| D. | 地球绕着太阳转 |
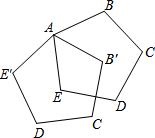 如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°.
如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=54°. 如图,△ABC沿BC方向平移到△DEF的位置,若EF=5cm,CE=2cm,则AD的长为3cm.
如图,△ABC沿BC方向平移到△DEF的位置,若EF=5cm,CE=2cm,则AD的长为3cm.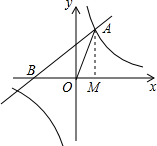 已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).
已知:如图,一次函数$y=\frac{{\sqrt{3}}}{3}x+m$与反比例函数$y=\frac{{\sqrt{3}}}{x}$的图象在第一象限的交点为A(1,n).