题目内容
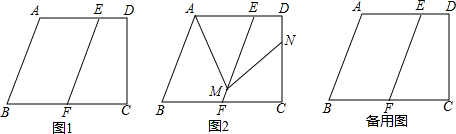
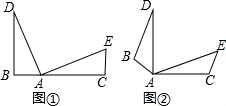
18.已知,如图1,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=11,CD=6,tan∠ABC=2,点E在AD边上,且AE=3ED,EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上.(1)求线段CF的长;
(2)如图2,当点M在线段FE上,且AM⊥MN,设FM•cos∠EFC=x,CN=y,求y关于x的函数解析式,并写出它的定义域;
(3)如果△AMN为等腰直角三角形,求线段FM的长.
分析 (1)过A作AH⊥BC,于是得到AH=CD=6,解直角三角形即可得到结论;
(2)过M作MP⊥CD于P,MK⊥BC于K,反向延长KM交AD于Q,则KQ⊥AD,解直角三角形求得MK=2x=PC,NP=y-2x,MP=CK=5-x=QD,于是得到AQ=8-(5-x)=3+x,QM=6-2x,推出△AMQ∽△PMN,根据相似三角形的性质列方程即可得到结论;
(3)①当M在线段EF上时,根据全等三角形的性质和等量代换得到QM=MP,列方程得到6-2x=5-x,解方程即可得到结论;②当M在FE的延长线上时,根据已知条件得到△AQM≌△MNH,由全等三角形的性质得到AQ=MH,由(2)知FK=x,CK=5-x=MH,MK=2x=CH,列方程即可得到结论.
解答 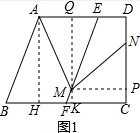 解:(1)过A作AH⊥BC,
解:(1)过A作AH⊥BC,
∴AH=CD=6,
∵tan∠ABC=2,
∴$\frac{AH}{BH}=2$,
∴BH=3,
∴CH=AD=8,
∴AE=$\frac{3}{4}×AD=6=BF$,
∴CF=5;
(2)过M作MK⊥BC于K,反向延长KM交AD于Q,则KQ⊥AD,在Rt△FMK中,FM•cos∠EFC=FK=x,
∵∠EFC=∠B,
∴tan∠EFC=2,
∴MK=2x=PC,NP=y-2x,MP=CK=5-x=QD
,∴AQ=8-(5-x)=3+x,QM=6-2x,
∵∠AMN=90°,
∵∠AMQ=∠PMN,∠AQM=∠MPN=90°,
∴△AMQ∽△PMN,
∴$\frac{AQ}{NP}=\frac{QM}{MP},即\frac{3+x}{y-2x}=\frac{6-2x}{5-x}$,
解得:y=$\frac{5{x}^{2}-14x-15}{2x-6}$(0≤x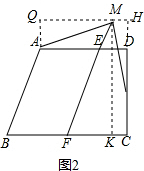 ≤1);
≤1);
(3)①当M在线段EF上时,
∵AM=MN,△AMQ≌△NMP,
∴△AMQ≌△NMP,
∴QM=MP,
∴6-2x=5-x,
∴x=1,
∴FM=$\frac{1}{cos∠B}=\frac{1}{\frac{1}{\sqrt{5}}}=\sqrt{5}$,
②当M在FE的延长线上时,
∵∠AMN=90°,
∴∠AMQ+∠NMH=∠NMH+∠MNH=90°,
∴∠AMQ=∠MNH,
在△AMQ与△NMH中,$\left\{\begin{array}{l}{∠Q=∠H=90°}\\{∠AMQ=∠NMH}\\{AM=MN}\end{array}\right.$,
∴△AQM≌△MNH,
∴AQ=MH,由(2)知FK=x,CK=5-x=MH,MK=2x,=CH,
∴AQ=DH=2x-6,∴2x-6=5-x,∴$x=\frac{11}{3}$,
∴FM=$\frac{\frac{11}{3}}{\frac{1}{\sqrt{5}}}$=$\frac{11}{3}\sqrt{5}$,
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,三角函数的定义,求函数的解析式,证明△AQM≌△MNH是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
| A. | m<2 | B. | m>2 | C. | m≥2 | D. | m≤2 |
 请从以下两个小题中个任意选一作答,若对选,则按第一题计分.
请从以下两个小题中个任意选一作答,若对选,则按第一题计分.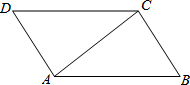 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.