题目内容
13.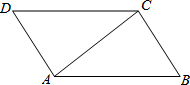 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.(1)请按如下步骤在图中完成作图(保留作图痕迹):
①分别以A,C为圆心,以大于$\frac{1}{2}AC$长为半径画弧,弧在AC两侧的交点分别为P,Q;②连结PQ,PQ分别与AB,AC,CD交于点E,O,F.
(2)再连接AF、CE,求证:四边形AECF是菱形.
分析 (1)根据要求画出图形即可;
(2)根据作图可得PQ是AC的垂直平分线,进而可得AO=CO,然后证明△OFC≌△OEA可得FC=AE,从而可得四边形AECF是平行四边形,再根据AC⊥EF可判定四边形AECF是菱形.
解答 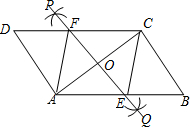 (1)解:如图所示;
(1)解:如图所示;
(2)证明:根据作图可得PQ是AC的垂直平分线,
∴AO=OC,
∵DC∥AB,
∴∠CFO=∠AEO,∠FCO=∠EAO,
在△OFC和△OEA中$\left\{\begin{array}{l}{∠CFO=∠AEO}\\{∠FCO=∠EAO}\\{AO=CO}\end{array}\right.$,
∴△OFC≌△OEA(AAS),
∴FC=AE,
∴四边形AECF是平行四边形,
∵AC⊥FE,
∴四边形AECF是菱形.
点评 此题主要考查了复杂作图,以及菱形的判定,关键是掌握线段垂直平分线的做法,掌握对角线互相垂直的平行四边形是菱形.

练习册系列答案
相关题目
3.计算(-2a)2的结果是( )
| A. | -4a2 | B. | 2a2 | C. | -2a2 | D. | 4a2 |
4.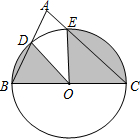 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
 如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )
如图,以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E.若∠A=80°,BC=4,则图中阴影部分图形的面积和为( )| A. | $\frac{64}{9}π$ | B. | $\frac{32}{9}π$ | C. | $\frac{16}{9}π$ | D. | $\frac{8}{9}π$ |
5.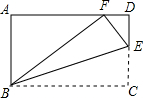 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
3.下列各式计算正确的是( )
| A. | a3+a4=a7 | B. | (3a+b)2=9a2+b2 | C. | (-ab3)2=a2b6 | D. | a6b÷a2=a3b |