题目内容
4. 如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )
如图,菱形ABCD的对角线BD长为4$\sqrt{3}$cm,高AE长为2$\sqrt{3}$cm,则菱形ABCD的周长为( )| A. | 20cm | B. | 16cm | C. | 12cm | D. | 8cm |
分析 由三角形ACB的面积为定值可求出AC=BC,再由菱形的性质可证明△ACB是等边三角形,所以∠ABC=60°,则AB的长可求出,进而可求出菱形ABCD的周长.
解答 解:
设AC和BD相交于点O,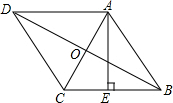
∵四边形ABCD是菱形,
∴BD⊥AC,BO=$\frac{1}{2}$BD=2$\sqrt{3}$cm,AB=BC=CD=AD,
∵高AE长为2$\sqrt{3}$cm,S△ABC=$\frac{1}{2}$AE•BC=$\frac{1}{2}$AC•BO,
∴BC=AC,
∴AC=BC=AB,
∴△ACB是等边三角形,
∴∠ABC=60°,
∵AE=2$\sqrt{3}$cm,
∴AB=4cm,
∴菱形ABCD的周长=4AB=16cm,
故选B.
点评 本题考查了菱形的性质、等边三角形的判定和性质以及三角形面积公式的运用,正确判定△ACB是等边三角形是解题的关键.

练习册系列答案
相关题目
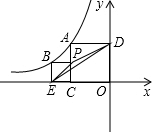 如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$.
如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$. 如图所示,每一个小方格都是边长为1个单位的正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
如图所示,每一个小方格都是边长为1个单位的正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(m,n).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(m,n). 如图,在矩形ABCD中,AB=10,BC=5,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为8.
如图,在矩形ABCD中,AB=10,BC=5,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为8.