题目内容
7.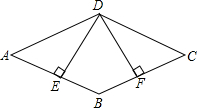 如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.
如图,四边形ABCD是平行四边形,DE⊥BC,垂足分别是E,F,且DE=FD.(1)求证:△AED≌△CFD;
(2)求证:四边形ABCD是菱形.
分析 (1)首先根据平行四边形的性质得出∠A=∠C,进而利用全等三角形的判定得出即可;
(2)根据菱形的判定得出即可.
解答 证明:(1)∵DE⊥AB,DF⊥BC
∴∠AED=∠CFD=90°,
∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AED和△CFD中,
$\left\{\begin{array}{l}{∠AED=∠CFD}\\{∠A=∠C}\\{DE=DF}\end{array}\right.$,
∴△AED≌△CFD(AAS);
(2)∵由(1)知,△AED≌△CFD,
∴AD=CD,
∵四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形.
点评 此题主要考查了菱形的性质和全等三角形的判定等知识,根据已知得出∠A=∠C是解题关键.

练习册系列答案
相关题目
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A(-2,1),则当x<-1时,函数值y的取值范围是( )
| A. | y>2 | B. | -2<y<0 | C. | y>-2 | D. | 0<y<2 |
18. 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )
 两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )
两个反比例函数y=$\frac{k}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{k}{x}$的图象于点B,当点P在y=$\frac{1}{x}$的图象上运动时,下列结论错误的是( )| A. | △ODB与△OCA的面积相等 | |
| B. | 当点A是PC的中点时,点B一定是PD的中点. | |
| C. | 只有当四边形OCPD为正方形时,四边形PAOB的面积最大 | |
| D. | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
17.若多项式a2+4a+k2是完全平方式,则常数k的值为( )
| A. | 2 | B. | 4 | C. | ±4 | D. | ±2 |
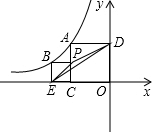 如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$.
如图,A,B(点B在点A左边)分别是反比例函数y=$\frac{k}{x}$(x<0)图象上的两,过点A作两坐标轴的垂线,得到正方形ACOD,过点B作x轴和AC的垂线,得到正方形BECP.连接EP和DE,已知△PED的面积为2,则k的值为-6-2$\sqrt{5}$. 如图所示,每一个小方格都是边长为1个单位的正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
如图所示,每一个小方格都是边长为1个单位的正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系. 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(m,n).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(m,n).