题目内容
19. 如图,已知O是△ABC内的一点,试说明:
如图,已知O是△ABC内的一点,试说明:(1)OB+OC<AB+AC;
(2)OA+OB+OC>$\frac{1}{2}$(AB+BC+AC).
分析 (1)延长BO交AC于D,在△ABD与△COD中根据三角形的三边关系即可得出结论;
(2)在△ABO和△AOC以及△BOC中,分别利用三角形三边关系定理,两边之和大于第三边,然后把三个式子相加即可证得.
解答 (1)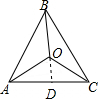 证明:延长BO交AC于D,
证明:延长BO交AC于D,
∵△ABD中,AB+AD>BD,即AB+AD>OB+OD,
△COD中,OD+CD>OC,
∴AB+AD+CD>OB+OD+CD>OB+OC,AB+AC>OB+OC;
(2)证明:∵△ABO中,OA+OB>AB,
同理,OA+OC>CA,OB+OC>BC.
∴2(OA+OB+OC)>AB+BC+AC,
∴OA+OB+OC>$\frac{1}{2}$(AB+BC+AC).
点评 本题考查三角形的三边关系,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
相关题目
14. 在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
 在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{π}{3}$ |
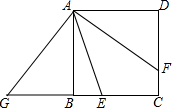 如图,在正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于点F,反向延长BC至G,使BG=DF,连接AG,求证:
如图,在正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于点F,反向延长BC至G,使BG=DF,连接AG,求证: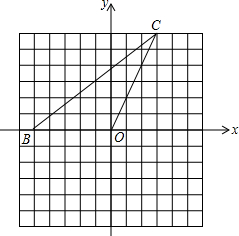 已知:如图,在平面直角坐标系中,点B(-5,0),点C(3,6),若点D是由点C平移得到,并且△OBD与△OBC的面积相等,请写出三个不同的点D的坐标.
已知:如图,在平面直角坐标系中,点B(-5,0),点C(3,6),若点D是由点C平移得到,并且△OBD与△OBC的面积相等,请写出三个不同的点D的坐标.