题目内容
11.在矩形ABCD中,对角线AC,BD相交于点O,矩形的边与对角线长之比为1:2,AE为∠BAD的角平分线,交矩形ABCD的一边于点E,联结OE,则∠BOE=75°.分析 由矩形的性质得出OA=OB,∠BAD=∠ABC=90°,证出AB=OA=OB,得出∠ABO=60°,∠OBE=30°,再证出△ABE是等腰直角三角形,得出BE=AB,因此BE=OB,由等腰三角形的性质和三角形内角和定理即可得出结果.
解答 解:如图所示: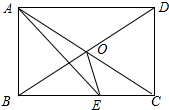
∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵AB:BD=1:2,
∴AB=OA=OB,
∴∠ABO=60°,
∴∠OBE=30°,
∵AE为∠BAD的角平分线,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴BE=AB,
∴BE=OB,
∴∠BOE=∠BEO=$\frac{1}{2}$(180°-30°)=75°,
故答案为:75°.
点评 本题考查了矩形的性质、等边三角形的判定、等腰直角三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
1.若$y=-\frac{1}{x}$图象与y=-x2+bx图象有且仅有2个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
| A. | x1+x2>0,y1+y2>0 | B. | x1+x2>0,y1+y2<0 | C. | x1+x2<0,y1+y2>0 | D. | x1+x2<0,y1+y2<0 |
20.点P在第四象限,点P到x轴的距离是4,到y轴的距离是2,则点P的坐标是( )
| A. | (4,2) | B. | (4,-2) | C. | (-2,4) | D. | (2,-4) |
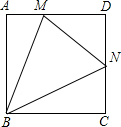 如图,在正方形ABCD中,N是DC的中点,M是AD上异于点D的点,且∠NMB=∠MBC,求$\frac{AM}{AB}$的值.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于点D的点,且∠NMB=∠MBC,求$\frac{AM}{AB}$的值. 如图,已知O是△ABC内的一点,试说明:
如图,已知O是△ABC内的一点,试说明: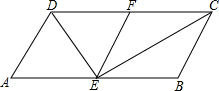 在四边形ABCD中,AD=BC,DE平分∠ADF,CE平分∠BCF,∠CDE+∠DCE=90°,E,F分别是AB,CD的中点.
在四边形ABCD中,AD=BC,DE平分∠ADF,CE平分∠BCF,∠CDE+∠DCE=90°,E,F分别是AB,CD的中点. 如图,△ABC三条角平分线AD、BE,CF交于点G,GH⊥BC于H,求证:∠BGD=∠CGH.
如图,△ABC三条角平分线AD、BE,CF交于点G,GH⊥BC于H,求证:∠BGD=∠CGH.