题目内容
10．已知：5x2-12xy+9y2-4x+4=0，求（y-x）-x的值．分析 已知等式变形后，利用非负数的性质求出x与y的值，即可确定出所求式子的值．
解答 解：∵5x2-12xy+9y2-4x+4=0，
∴4x2-12xy+9y2+x2-4x+4=0，
∴（2x-3y）2+（x-2）2=0，
∴2x-3y=0，x-2=0，
解得：x=2，y=$\frac{4}{3}$，
∴（y-x）-x=9．
点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
1．若$y=-\frac{1}{x}$图象与y=-x2+bx图象有且仅有2个不同的公共点A（x1，y1），B（x2，y2），则下列判断正确的是（ ）
| A． | x1+x2＞0，y1+y2＞0 | B． | x1+x2＞0，y1+y2＜0 | C． | x1+x2＜0，y1+y2＞0 | D． | x1+x2＜0，y1+y2＜0 |
如图，点A（-3，0），B（0，2），将三角形AOB向右平移5个单位长度，再向下平移2个单位长度得到三角形CDE，点A、O、B的对应点分别为C、D、E．点P从点O开始水平向右平移，点Q从点D开始水平向左平移，速度均为每秒2个单位长度，运动时间为t秒．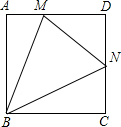
如图，在正方形ABCD中，N是DC的中点，M是AD上异于点D的点，且∠NMB=∠MBC，求$\frac{AM}{AB}$的值．
如图，已知O是△ABC内的一点，试说明：
20．点P在第四象限，点P到x轴的距离是4，到y轴的距离是2，则点P的坐标是（ ）
| A． | （4，2） | B． | （4，-2） | C． | （-2，4） | D． | （2，-4） |