题目内容
四边形ABCD是正方形．
(1)如图(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；
(2)在(1)中，线段EF与AF，BF的等量关系是____；(不需证明，直接写出结论即可)
(3)如图(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是____，线段EF与AF，BF的等量关系是____．(不需证明，直接写出结论即可)
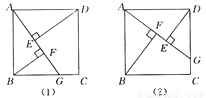
EF＝AF－BF △ABF≌△DAE EF＝BF－AF
【解析】试题分析：（1）根据正方形的性质可知：△ABF≌△ADE；
（2）利用全等三角形的性质，AE=BF，AF=DE，得出AF-BF=EF；
（3）同理可得出图（2），△ABF≌△DAE，EF=BF-AF．
(1) 证明：在正方形ABCD中，AB＝AD，∠BAD＝90°，
∴∠BAF+∠DAE＝90°．
...
阅读快车系列答案已知锐角A的正弦sin A是一元二次方程2x2－7x＋3＝0的根，则sin A＝________．
【解析】2x2－7x＋3＝0，
（2x-1）(x-3)=0，
∴，
∵sinA<1，
∴sinA=，
故答案为： . 如图所示，下列每组图形中的两个三角形不是通过平移得到的是 ( )
A.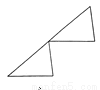 
B.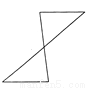 
C.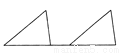 
D.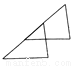 
B
【解析】试题分析：A、C、D可以通过平移得到，
B可以通过旋转得到，
故选B． 直角三角形两锐角的平分线所夹的钝角的度数为（ ）
A. 100度 B. 120度 C. 135度 D. 140度
C
【解析】【解析】
如图，∵∠C=90°，∴∠BAC+∠ABC=180°﹣90°=90°．
∵AD、BE分别是∠BAC和∠ABC的平分线，∴∠OAB+∠OBA=×90°=45°，
∴∠AOB=180°﹣（∠OAB+∠OBA）=180°﹣45°=135°．故选C． Rt△ABC中，∠C=90°，∠B=46°，则∠A=（ ）
A. 44° B. 34° C. 54° D. 64°
A
【解析】【解析】
∵∠C=90°，∠B=46°，∴∠A=90°﹣46°=44°．故选A． 下面几种三角形：
①有两个角为60°的三角形；
②三个外角都相等的三角形；
③一条边上的高也是这条边上的中线的三角形；
④有一个角为60°的等腰三角形．
其中是等边三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】对于①，有两个角为60°的三角形为等边三角形，故①正确；
对于②，三个外角都相等的三角形为等边三角形，故②正确；
对于③，一条边上的高也是这条边上的中线的三角形有可能是等腰三角形或等边三角形，故③错误；
对于④，有一个角为60° 的等腰三角形为等边三角形，故④正确.
综上，①②④所述为等边三角形.
故选B. 已知Rt△ABC中，∠C=90°，BC=4，AC=4，现将△ABC沿CB方向平移到△A’B’C’的位置，若平移距离为3，求△ABC与△A’B’C’的重叠部分的面积？
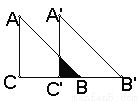
4.5.
【解析】因为∠C＝90°，BC＝4，AC＝4，所以△ABC是等腰直角三角形，可得重叠部分也是等腰直角三角形．又因为平移距离为3，所以C′B＝4－3＝1，所以重叠部分的面积为． 如图所示的每个图形中的两个三角形是经过平移得到的是（ ）
A.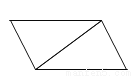 
B.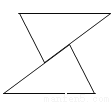 
C.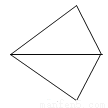 
D.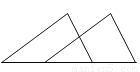 
D
【解析】试题解析：根据平移的特征,只有D选项是三角形的平移而成.
故选D. 如果三角形的三个内角度数比为1：1：2，则这个三角形为（ ）
A. 锐角三角形 B. 钝角三角形
C. 非等腰直角三角形 D. 等腰直角三角形
D
【解析】【解析】
∵三角形的三个内角度数比为1：1：2，∴设三角形的三个内角分别为：x，x，2x，∴x+x+2x=180°，解得：x=45°，∴三角形的三个内角度数分别为：45°，45°，90°，∴这个三角形为等腰直角三角形．故选D．