��Ŀ����
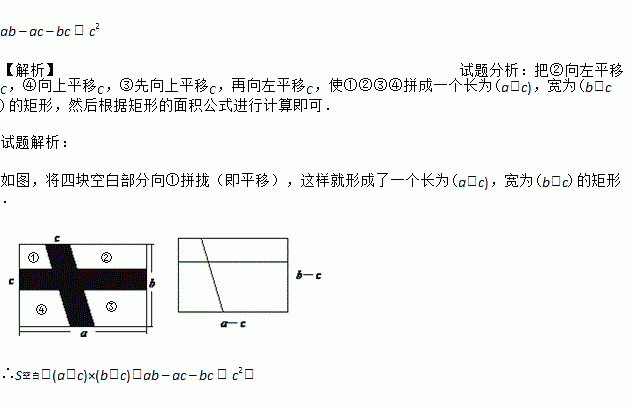
�ھ���ABCD�У�������Ӱ�����Ǿ��Σ���һ��Ӱ������ƽ���ı��Σ�����ͼ�б�ע�����ݣ��������հײ��ֵ������

 ab �C ac �C bc �� c2
������������������Ѣ�����ƽ��c��������ƽ��c����������ƽ��c��������ƽ��c��ʹ�٢ڢۢ�ƴ��һ����Ϊ(a��c)����Ϊ(b��c)�ľ��Σ�Ȼ����ݾ��ε������ʽ���м��㼴�ɣ�
���������
��ͼ�����Ŀ�հײ������ƴ£����ƽ�ƣ����������γ���һ����Ϊ(a��c)����Ϊ(b��c)�ľ��Σ�
��S�հף�(a��c)��(b��c)��ab �C ac �C bc ...
ab �C ac �C bc �� c2
������������������Ѣ�����ƽ��c��������ƽ��c����������ƽ��c��������ƽ��c��ʹ�٢ڢۢ�ƴ��һ����Ϊ(a��c)����Ϊ(b��c)�ľ��Σ�Ȼ����ݾ��ε������ʽ���м��㼴�ɣ�
���������
��ͼ�����Ŀ�հײ������ƴ£����ƽ�ƣ����������γ���һ����Ϊ(a��c)����Ϊ(b��c)�ľ��Σ�
��S�հף�(a��c)��(b��c)��ab �C ac �C bc ...
��ϰ��ϵ�д�
�����Ŀ
��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��DE��AB��E��DF��AC��F��MΪAD������һ�㣬�����н����д������( )
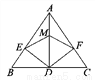
A. DE��DF B. ME��MF
C. AE��AF D. BD��CD
 D
����������ADƽ�֡�BAC��DE��AB��DF��AC��
���BAD=��CAD����AED=��AFD=90�㣬
�֡�AD=AD��
���ADE�ա�ADF��
��DE=DF��AE=AF��
��AE=AF����BAD=��CAD��AM=AM��
���AME�ա�AMF��
��ME=MF��
��ѡ��A��B��C��ȷ��
���õ�BD=CD����ѡ��D����
��ѡD...
D
����������ADƽ�֡�BAC��DE��AB��DF��AC��
���BAD=��CAD����AED=��AFD=90�㣬
�֡�AD=AD��
���ADE�ա�ADF��
��DE=DF��AE=AF��
��AE=AF����BAD=��CAD��AM=AM��
���AME�ա�AMF��
��ME=MF��
��ѡ��A��B��C��ȷ��
���õ�BD=CD����ѡ��D����
��ѡD... ��֪���A������sin A��һԪ���η���2x2��7x��3��0�ĸ�����sin A��________��
 ��������2x2��7x��3��0��
��2x-1��(x-3)=0��
�࣬
��sinA<1��
��sinA=��
�ʴ�Ϊ�� .
��������2x2��7x��3��0��
��2x-1��(x-3)=0��
�࣬
��sinA<1��
��sinA=��
�ʴ�Ϊ�� . �ֽ���ʽ��2a2b��5ab2
 ab(2a��5b)
����������������������ṫ��ʽ���ֽ���ʽ����ȷ������ʽab������ȡ����ʽ����.
���������2a2b��5ab2= ab(2a��5b).
ab(2a��5b)
����������������������ṫ��ʽ���ֽ���ʽ����ȷ������ʽab������ȡ����ʽ����.
���������2a2b��5ab2= ab(2a��5b). �Ѷ���ʽ(x��2)2��4x��8�ֽ���ʽ����һ����ʼ�����˴���( )
��������
ԭʽ��(x��2)2��(4x��8)��A
��(x��2)2��4(x��2)��B
��(x��2)(x��2��4)��C
��(x��2)(x��2)��D
 C
���������������⣬��һ��Ӧ�������ţ�ע����ű仯�����ⷨ��ȷ���ڶ����ȶԺ�����ʽ�ṫ��ʽ4������ȡ����ʽ��x-2����ʱ���ַ��Ŵ������Դ�C�����ִ���.
��ѡ��C.
C
���������������⣬��һ��Ӧ�������ţ�ע����ű仯�����ⷨ��ȷ���ڶ����ȶԺ�����ʽ�ṫ��ʽ4������ȡ����ʽ��x-2����ʱ���ַ��Ŵ������Դ�C�����ִ���.
��ѡ��C. ��ͼ��ʾ��AD��BC����ABC��80�㣬��BCD��50�㣬����ƽ�Ƶ�֪ʶ����BC��AD+AB��������ϵ��
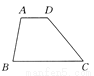
 BC��AD+AB��
�������������������ABƽ����DE��λ�ã���ƽ�Ƶ����ʿɵã�AB��DE��AD��BE����DEC����ABC��80�㣬�ڡ�DEC�����������ε��ڽǺͶ����ɵá�CDE����BCD��50�㣬���ɵȽǶԵȱߵó�DE��EC�������������ɵó����ۣ�
���������
��������
����AD��BC��
���Կ�ƽ��AB��DE��λ��(����D����DE��AB��BC�ڵ�E)��
��AB��D...
BC��AD+AB��
�������������������ABƽ����DE��λ�ã���ƽ�Ƶ����ʿɵã�AB��DE��AD��BE����DEC����ABC��80�㣬�ڡ�DEC�����������ε��ڽǺͶ����ɵá�CDE����BCD��50�㣬���ɵȽǶԵȱߵó�DE��EC�������������ɵó����ۣ�
���������
��������
����AD��BC��
���Կ�ƽ��AB��DE��λ��(����D����DE��AB��BC�ڵ�E)��
��AB��D... ��ͼ��ʾ������ÿ��ͼ���е����������β���ͨ��ƽ�Ƶõ����� ( )
A. 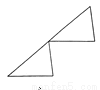
B. 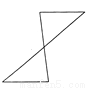
C. 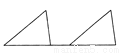
D. 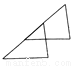
 B
�����������������A��C��D����ͨ��ƽ�Ƶõ���
B����ͨ����ת�õ���
��ѡB��
B
�����������������A��C��D����ͨ��ƽ�Ƶõ���
B����ͨ����ת�õ���
��ѡB�� ֱ������������ǵ�ƽ�������еĶ۽ǵĶ���Ϊ��������
A. 100�� B. 120�� C. 135�� D. 140��
 C
����������������
��ͼ���ߡ�C=90�㣬���BAC+��ABC=180�㩁90��=90�㣮
��AD��BE�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ����OAB+��OBA=��90��=45�㣬
���AOB=180�㩁����OAB+��OBA��=180�㩁45��=135�㣮��ѡC��
C
����������������
��ͼ���ߡ�C=90�㣬���BAC+��ABC=180�㩁90��=90�㣮
��AD��BE�ֱ��ǡ�BAC�͡�ABC��ƽ���ߣ����OAB+��OBA=��90��=45�㣬
���AOB=180�㩁����OAB+��OBA��=180�㩁45��=135�㣮��ѡC�� ��ͼ��ʾ��ÿ��ͼ���е������������Ǿ���ƽ�Ƶõ����ǣ� ��
A. 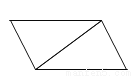
B. 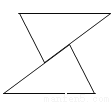
C. 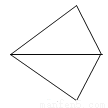
D. 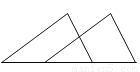
 D
���������������������ƽ�Ƶ�����,ֻ��Dѡ���������ε�ƽ�ƶ���.
��ѡD.
D
���������������������ƽ�Ƶ�����,ֻ��Dѡ���������ε�ƽ�ƶ���.
��ѡD.