题目内容
分式方程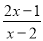 =1的解为( )
=1的解为( )
A. x=﹣1 B. x=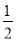 C. x=1 D. x=2
C. x=1 D. x=2
 A
【解析】【解析】
去分母得:2x﹣1=x﹣2,
解得:x=﹣1,
经检验x=﹣1是分式方程的解,
则分式方程的解为x=﹣1.
故选:A.
A
【解析】【解析】
去分母得:2x﹣1=x﹣2,
解得:x=﹣1,
经检验x=﹣1是分式方程的解,
则分式方程的解为x=﹣1.
故选:A.
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
用“>”或“<”填空:
(1)如果x-2<3,那么x______5; (2)如果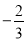 x<-1,那么x______
x<-1,那么x______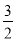 ;
;
(3)如果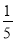 x>-2,那么x______-10;(4)如果-x>1,那么x______-1.
x>-2,那么x______-10;(4)如果-x>1,那么x______-1.
 < > > <
【解析】(1)如果x-2<3,那么x<5;
(2)如果,那么;
(3)如果,那么x>-10;
(4)如果-x>1,那么x<-1.
< > > <
【解析】(1)如果x-2<3,那么x<5;
(2)如果,那么;
(3)如果,那么x>-10;
(4)如果-x>1,那么x<-1. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,M为AD上任意一点,则下列结论中错误的是( )
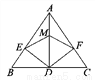
A. DE=DF B. ME=MF
C. AE=AF D. BD=CD
 D
【解析】∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠BAD=∠CAD,∠AED=∠AFD=90°,
又∵AD=AD,
∴△ADE≌△ADF,
∴DE=DF,AE=AF,
∵AE=AF,∠BAD=∠CAD,AM=AM,
∴△AME≌△AMF,
∴ME=MF,
故选项A、B、C正确,
无法得到BD=CD,故选项D错误,
故选D...
D
【解析】∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠BAD=∠CAD,∠AED=∠AFD=90°,
又∵AD=AD,
∴△ADE≌△ADF,
∴DE=DF,AE=AF,
∵AE=AF,∠BAD=∠CAD,AM=AM,
∴△AME≌△AMF,
∴ME=MF,
故选项A、B、C正确,
无法得到BD=CD,故选项D错误,
故选D... 如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )

A. 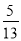 B.
B. 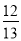 C.
C. 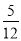 D.
D. 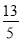
 A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B.
A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B. 请你给x选择一个合适的值,使方程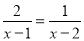 成立,你选择的x=__.
成立,你选择的x=__.
 3
【解析】试题解析:方程两边可同乘(x?1)(x?2),得
2(x?2)=x?1,
解得x=3.
经检验x=3是原方程的解.
故答案为:3.
3
【解析】试题解析:方程两边可同乘(x?1)(x?2),得
2(x?2)=x?1,
解得x=3.
经检验x=3是原方程的解.
故答案为:3. 如图,已知?ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=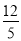 ,求CF的长.
,求CF的长.
 (1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边...
(1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边... 已知锐角A的正弦sin A是一元二次方程2x2-7x+3=0的根,则sin A=________.
 【解析】2x2-7x+3=0,
(2x-1)(x-3)=0,
∴,
∵sinA<1,
∴sinA=,
故答案为: .
【解析】2x2-7x+3=0,
(2x-1)(x-3)=0,
∴,
∵sinA<1,
∴sinA=,
故答案为: . 分解因式:2a2b-5ab2
 ab(2a-5b)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2a2b-5ab2= ab(2a-5b).
ab(2a-5b)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2a2b-5ab2= ab(2a-5b). 直角三角形两锐角的平分线所夹的钝角的度数为( )
A. 100度 B. 120度 C. 135度 D. 140度
 C
【解析】【解析】
如图,∵∠C=90°,∴∠BAC+∠ABC=180°﹣90°=90°.
∵AD、BE分别是∠BAC和∠ABC的平分线,∴∠OAB+∠OBA=×90°=45°,
∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣45°=135°.故选C.
C
【解析】【解析】
如图,∵∠C=90°,∴∠BAC+∠ABC=180°﹣90°=90°.
∵AD、BE分别是∠BAC和∠ABC的平分线,∴∠OAB+∠OBA=×90°=45°,
∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣45°=135°.故选C. 
