题目内容
已知∠AOB及其内部一点P,试讨论以下问题的解答:
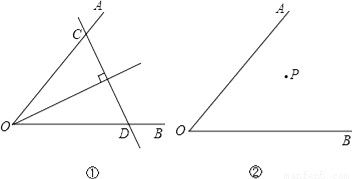
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
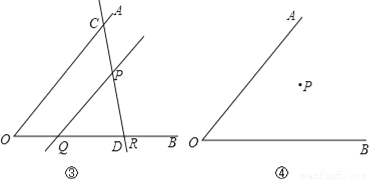
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.
 (1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:【解析】
(1)能.
...
(1)能,画法见解析;(2)理由见解析;(3)见解析.
【解析】试题分析:(1)作∠AOB的平分线,过P点作角平分线的垂线,分别交角的两边OA、OB于点C、D,则△OCD是以CD为底边的等腰三角形;
(2)根据PQ∥OA,得出∠QPR=∠OCD,进而得出OD=CD,即可得出答案;
(3)作QP∥DO,再作∠ODR=∠O,即可得出答案.
试题解析:【解析】
(1)能.
...
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案直角三角形两锐角的平分线所夹的钝角的度数为( )
A. 100度 B. 120度 C. 135度 D. 140度
 C
【解析】【解析】
如图,∵∠C=90°,∴∠BAC+∠ABC=180°﹣90°=90°.
∵AD、BE分别是∠BAC和∠ABC的平分线,∴∠OAB+∠OBA=×90°=45°,
∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣45°=135°.故选C.
C
【解析】【解析】
如图,∵∠C=90°,∴∠BAC+∠ABC=180°﹣90°=90°.
∵AD、BE分别是∠BAC和∠ABC的平分线,∴∠OAB+∠OBA=×90°=45°,
∴∠AOB=180°﹣(∠OAB+∠OBA)=180°﹣45°=135°.故选C. 如图所示的每个图形中的两个三角形是经过平移得到的是( )
A. 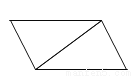
B. 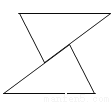
C. 
D. 
 D
【解析】试题解析:根据平移的特征,只有D选项是三角形的平移而成.
故选D.
D
【解析】试题解析:根据平移的特征,只有D选项是三角形的平移而成.
故选D. x=-1不是下列哪一个不等式的解( )
A. 2x+1≤-3 B. 2x-1≥-3 C. -2x+1≥3 D. -2x-1≤3
 A
【解析】由不等式2x+1<-3可得x<-2,所以x=-1不是不等式2x+1<-3的解;由2x-1≥-3的解集为x≥-1,可知x=-1是不等式2x+1≥-3的解;由-2x+1≥3的解集为x≤-1,可知x=-1是不等式-2x+1≥3的解;由-2x-1≤3的解集为x≥-1,可知x=-1是不等式-2x-1≤3的解.
故选:A.
A
【解析】由不等式2x+1<-3可得x<-2,所以x=-1不是不等式2x+1<-3的解;由2x-1≥-3的解集为x≥-1,可知x=-1是不等式2x+1≥-3的解;由-2x+1≥3的解集为x≤-1,可知x=-1是不等式-2x+1≥3的解;由-2x-1≤3的解集为x≥-1,可知x=-1是不等式-2x-1≤3的解.
故选:A. 不等式(a-2012)x>a-2012的解集是x<1.则a应满足的条件是( )
A. a=2012 B. a<2012 C. a>2012 D. 无法确定
 B
【解析】由含有a的不等式(a-2012)x>a-2012的解集为:x<1,根据不等式的基本性质3,可知a-2012<0,解得a<2012.
故选:B.
B
【解析】由含有a的不等式(a-2012)x>a-2012的解集为:x<1,根据不等式的基本性质3,可知a-2012<0,解得a<2012.
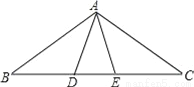
故选:B. 如图所示,在△ABC中,AB=AC,点D、E在BC边上,∠ABD=∠DAE=∠EAC=36°,则图中共有等腰三角形的个数是__.
 6
【解析】【解析】
∵AB=AC,∠ABD=36°,即△ABC是等腰三角形,∴∠C=∠B=36°,∴∠BAC=108°.
∵∠DAE=∠EAC=36°,∴∠BAD=36°,∴∠BAD=∠B=36°,∠EAC=∠C=36°,∴△ABD,△ACE是等腰三角形,∴∠ADE=∠AED=∠DAC=∠BAE=72°,∴△ADE,△ABE,△ACD是等腰三角形.
故答案为:6.
...
6
【解析】【解析】
∵AB=AC,∠ABD=36°,即△ABC是等腰三角形,∴∠C=∠B=36°,∴∠BAC=108°.
∵∠DAE=∠EAC=36°,∴∠BAD=36°,∴∠BAD=∠B=36°,∠EAC=∠C=36°,∴△ABD,△ACE是等腰三角形,∴∠ADE=∠AED=∠DAC=∠BAE=72°,∴△ADE,△ABE,△ACD是等腰三角形.
故答案为:6.
... 如果三角形的三个内角度数比为1:1:2,则这个三角形为( )
A. 锐角三角形 B. 钝角三角形
C. 非等腰直角三角形 D. 等腰直角三角形
 D
【解析】【解析】
∵三角形的三个内角度数比为1:1:2,∴设三角形的三个内角分别为:x,x,2x,∴x+x+2x=180°,解得:x=45°,∴三角形的三个内角度数分别为:45°,45°,90°,∴这个三角形为等腰直角三角形.故选D.
D
【解析】【解析】
∵三角形的三个内角度数比为1:1:2,∴设三角形的三个内角分别为:x,x,2x,∴x+x+2x=180°,解得:x=45°,∴三角形的三个内角度数分别为:45°,45°,90°,∴这个三角形为等腰直角三角形.故选D. 下列式子能用提公因式法分解因式的是( )
A. 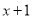 B.
B. 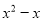 C.
C. 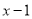 D.
D. 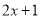
 B
【解析】根据提公因式法因式分解,可由,知B是因式分解.
故选:B.
B
【解析】根据提公因式法因式分解,可由,知B是因式分解.
故选:B. 如图,已知AB=AC=12 cm,AE=AF=7 cm,CE=10 cm,△ABF的周长是_________.
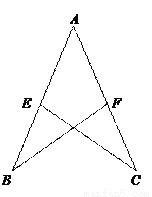
 29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm.
29cm
【解析】∵AB=AC,AE=AF=7(已知),∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长=AB+BF+FA=12+7+10=29(cm)
故答案为:29cm. 
