题目内容

4．若x1，x2是方程x2-x-2015=0的两个实数根，则$3{x_1}+{（{{x_2}+1}）^2}$的值是2019．

分析 先利用一元二次方程根的定义得到x22=x2+2015=0，则$3{x_1}+{（{{x_2}+1}）^2}$可化简为3（x1+x2）+2016，然后根据根与系数的关系得到x1+x2=1，再利用整体代入的方法计算．

解答 解：∵x2是方程x2-x-2015=0的实数根，
∴x22-x2-2015=0，
∴x22=x2+2015=0，
∴$3{x_1}+{（{{x_2}+1}）^2}$=3x1+x22+2x2+1
=3x1+x2+2015+2x2+1
=3（x1+x2）+2016，
∵x1，x2是方程x2-x-2015=0的两个实数根，
∴x1+x2=1，
∴$3{x_1}+{（{{x_2}+1}）^2}$=3（x1+x2）+2016=3×1+2016=2019．
故答案为2019．

点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．也考查了一元二次方程解的定义．

练习册系列答案
相关题目
14．若关于x的不等式组$\left\{\begin{array}{l}{x-m＜0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个，则关于x的一元二次方程8x2-8x+m=0的根的情况是（　　）
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．有一个实数根
15．计算：
（1）$\frac{3}{20}×\sqrt{0.04}-\frac{1}{50}×\sqrt{0.0196}-\sqrt{0.01}$； 
（2）$\frac{1}{2}（{1+\frac{1}{2}}）（{1+\frac{1}{2^2}}）（{1+\frac{1}{2^4}}）（{1+\frac{1}{2^8}}）+\frac{1}{{2^{16}}}$．
12．若A和B都是3次多项式，则A+B一定是（　　）
A．6次多项式B．3次多项式
C．次数不高于3次的多项式D．次数不低于3次的多项式
19．函数y=（m2-m）${x}^{{m}^{2}-3m+1}$是反比例函数，则（　　）
A．m≠0B．m≠0且m≠1C．m=2D．m=1或2
9．探索：小明和小亮在研究一个数学问题：已知AB∥CD，AB和CD都不经过点P，探索∠P与∠A、∠的数量关系．
发现：在图1中，小明和小亮都发现：∠APC=∠A+∠C；

小明是这样证明的：过点P作PQ∥AB
∴∠APQ=∠A（两直线平行，内错角相等）
∵PQ∥AB，AB∥CD．
∴PQ∥CD（平行于同一直线的两直线平行）
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的：过点作PQ∥AB∥CD．
∴∠APQ=∠A，∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上，填写依据；两人的证明过程中，完全正确的是小明的证法．
应用：
在图2中，若∠A=120°，∠C=140°，则∠P的度数为100°；
在图3中，若∠A=30°，∠C=70°，则∠P的度数为40°；
拓展：
在图4中，探索∠P与∠A，∠C的数量关系，并说明理由．
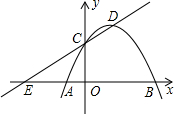16．如图，已知抛物线y=ax2+bx+c（a＜0）经过点A（-1，0），B（3，0），且与y轴交于点C，点D为顶点，直线CD与x轴交于点E，以DE为腰作等腰Rt△DEF，若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$．
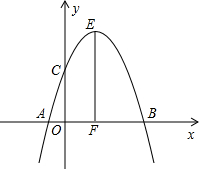13．先化简，再求值：1+$\frac{1-a}{a}$$÷\frac{{a}^{2}-1}{{a}^{2}+2a}$，其中a=$\sqrt{2}$-1．
3．如图，抛物线y=-x2+2x+3经过点A、B、C，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，则实数m的变化范围为-$\frac{5}{4}$≤m≤5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网