Question

18．如图，AB是⊙O的直径，F是⊙O外一点，FC切⊙O于点C，过点F作FD⊥AB于点D，交弦AC于点E．
（1）求证：EF=CF；
（2）若AB=10，DF=6，cos∠FCE=$\frac{3}{5}$，求线段AE的长．

Answer 1

分析 （1）连接半径OC，根据切线可得：∠FCO=90°，由同圆的半径相等和垂直的定义得：∠FCA=∠AED，
根据对顶角相等，进行等量代换可得：∠FEC=∠FCA，所以EF=CF；
（2）根据同角的三角函数得：cos∠AED=$\frac{3}{5}$，设DE=3x，AE=5x，则AD=4x，FE=FC=6-3x，证明△FEC∽△OBC，则$\frac{FE}{OB}=\frac{EC}{BC}$，表示EC=$\frac{6（6-3x）}{5}$，根据AC=AE+EC列式可求得x的值，

解答 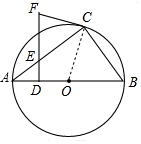证明：（1）连接OC，
∵FC切⊙O于点C，
∴∠FCO=90°，
∴∠FCA+∠ACO=90°，
∵OA=OC，
∴∠A=∠ACO，
∴∠FCA+∠A=90°，
∵FD⊥AB，
∴∠FDA=90°，
∴∠AED+∠A=90°，
∴∠FCA=∠AED，
∵∠AED=∠FEC，
∴∠FEC=∠FCA，
∴EF=CF；
（2）由（1）得∠AED=∠FCE，
∵cos∠FCE=$\frac{3}{5}$，
∴cos∠AED=$\frac{3}{5}$，
设DE=3x，AE=5x，则AD=4x，
∴FE=FC=6-3x，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠ACO+∠BCO=90°，
∵∠FCE+∠ACO=90°，
∴∠BCO=∠FCE，
∵OB=OC，
∴∠OCB=∠OBC，
∴∠FCE=∠FEC=∠OCB=∠OBC，
∴△FEC∽△OBC，
∴$\frac{FE}{OB}=\frac{EC}{BC}$，
Rt△ABC中，∠B=∠AED，
∴cos∠B=$\frac{3}{5}$=$\frac{BC}{AB}$，
∵AB=10，
∴BC=6，
∴AC=8，
∴$\frac{6-3x}{5}=\frac{EC}{6}$，
∴EC=$\frac{6（6-3x）}{5}$，
∵AC=AE+EC=8，
∴5x+$\frac{6（6-3x）}{5}$=8，
x=$\frac{4}{7}$，
∴AE=5x=$\frac{20}{7}$．

点评 本题考查了切线的性质、三角函数、相似三角形的性质和判定等，熟记圆的切线垂直于过切点的半径，明确直径所对的圆周角是直角，在几何证明中，如果已知某角的三角函数值，可以根据函数定义列比例式或根据此条件设未知数，利用勾股定理或相似列等式可求解．