题目内容
6.计算:(1)(+1.5)+(+6.1);
(2)(-$\frac{5}{3}$)+(+$\frac{2}{3}$);
(3)(-$\frac{17}{42}$)+(+$\frac{5}{42}$);
(4)(+$\frac{31}{8}$)+(-$\frac{17}{4}$);
(5)(-6.25)+(+3.75);
(6)(+4.25)+(-$\frac{27}{4}$);
(7)(-$\frac{5}{9}$)+(-$\frac{2}{3}$);
(8)(-$\frac{3}{2}$)+(+$\frac{8}{3}$).
分析 有理数加法法则:
①同号相加,取相同符号,并把绝对值相加.
②绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
③一个数同0相加,仍得这个数.
解答 解:(1)(+1.5)+(+6.1)=7.6;
(2)(-$\frac{5}{3}$)+(+$\frac{2}{3}$)=-1;
(3)(-$\frac{17}{42}$)+(+$\frac{5}{42}$)=-$\frac{2}{7}$;
(4)(+$\frac{31}{8}$)+(-$\frac{17}{4}$)=-$\frac{3}{8}$;
(5)(-6.25)+(+3.75)=-2.5;
(6)(+4.25)+(-$\frac{27}{4}$)=-2.5;
(7)(-$\frac{5}{9}$)+(-$\frac{2}{3}$)=-$\frac{11}{9}$;
(8)(-$\frac{3}{2}$)+(+$\frac{8}{3}$)=$\frac{7}{6}$.
点评 此题考查了有理数的加法,在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0.从而确定用那一条法则.在应用过程中,要牢记“先符号,后绝对值”.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
 如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 3 |
16.先化简,再求代数式的值:($\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$)÷$\frac{a}{a-1}$=( ),其中a=tan60°-2sin30°.
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{5}$ |
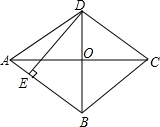 如图,菱形ABCD,AC,BD相交于点O,DE⊥AB,垂足为E,AB=5,OD=3,求AC、DE的长.
如图,菱形ABCD,AC,BD相交于点O,DE⊥AB,垂足为E,AB=5,OD=3,求AC、DE的长. 如图,AB是⊙O的直径,F是⊙O外一点,FC切⊙O于点C,过点F作FD⊥AB于点D,交弦AC于点E.
如图,AB是⊙O的直径,F是⊙O外一点,FC切⊙O于点C,过点F作FD⊥AB于点D,交弦AC于点E. 为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,则这棵古杉树AB的长为18m.(结果取整数)(参考数据:$\sqrt{2}$=1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,则这棵古杉树AB的长为18m.(结果取整数)(参考数据:$\sqrt{2}$=1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)