题目内容
13.若关于x的一元二次方程x2-4x+m=0有实数根,则实数m满足m≤4.分析 根据方程有实数根结合根的判别式即可得出关于m的一元一次不等式,解不等式即可得出结论.
解答 解:∵方程x2-4x+m=0有实数根,
∴△=(-4)2-4m=16-4m≥0,
解得:m≤4.
故答案为:m≤4.
点评 本题考查了根的判别式,熟练掌握“当△≥0时,方程有实数根.”是解题的关键.

练习册系列答案
相关题目
3.a${\;}^{-\frac{1}{2}}$(a>0)等于( )
| A. | $\sqrt{a}$ | B. | -$\sqrt{a}$ | C. | $\frac{\sqrt{a}}{a}$ | D. | -$\frac{\sqrt{a}}{a}$ |
8.-$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
5.若实数a满足a-|a|=2a,则( )
| A. | a≤0 | B. | a<0 | C. | a>0 | D. | a≥0 |
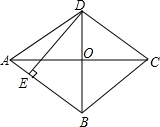 如图,菱形ABCD,AC,BD相交于点O,DE⊥AB,垂足为E,AB=5,OD=3,求AC、DE的长.
如图,菱形ABCD,AC,BD相交于点O,DE⊥AB,垂足为E,AB=5,OD=3,求AC、DE的长. 如图,AB是⊙O的直径,F是⊙O外一点,FC切⊙O于点C,过点F作FD⊥AB于点D,交弦AC于点E.
如图,AB是⊙O的直径,F是⊙O外一点,FC切⊙O于点C,过点F作FD⊥AB于点D,交弦AC于点E. 如图,已知AB∥CD,∠EBA=45°,∠E+∠D的度数为45°.
如图,已知AB∥CD,∠EBA=45°,∠E+∠D的度数为45°.