题目内容
9.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,掷一次这枚骰子,向上的一面的点数小于3的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
分析 由于一枚质地均匀的正方体骰子,骰子向上的一面点数可能为1、2、3、4、5、6,共有6种可能,小于3的点数有1、2,则根据概率公式可计算出骰子向上的一面点数小于3的概率.
解答 解:掷一枚质地均匀的正方体骰子,骰子向上的一面点数共有6种可能,而只有出现点数为1、2才小于3,
所以这个骰子向上的一面的点数小于3的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故选:B.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
相关题目
17. 如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
 如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 3 |
 如图,在△ABC中,∠C=90°,AC=3,BC=2,边AB的垂直平分线交AC边于点D,交AB边于点E,联结DB,那么tan∠DBC的值是$\frac{5}{12}$.
如图,在△ABC中,∠C=90°,AC=3,BC=2,边AB的垂直平分线交AC边于点D,交AB边于点E,联结DB,那么tan∠DBC的值是$\frac{5}{12}$. 如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC=$\frac{1}{3}$.
如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC=$\frac{1}{3}$.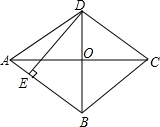 如图,菱形ABCD,AC,BD相交于点O,DE⊥AB,垂足为E,AB=5,OD=3,求AC、DE的长.
如图,菱形ABCD,AC,BD相交于点O,DE⊥AB,垂足为E,AB=5,OD=3,求AC、DE的长. 如图,AB是⊙O的直径,F是⊙O外一点,FC切⊙O于点C,过点F作FD⊥AB于点D,交弦AC于点E.
如图,AB是⊙O的直径,F是⊙O外一点,FC切⊙O于点C,过点F作FD⊥AB于点D,交弦AC于点E.