题目内容
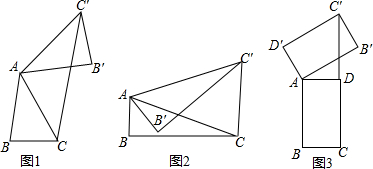
10.一个长方形台球桌面ABCD(AB∥CD,AD∥BC,∠A=90)如图1所示,已知台球在与台球桌边沿碰撞的过程中,撞击线路与桌边的夹角等于反射线路与桌边的夹角,如∠1=∠2(1)台球经过如图2的两次反弹后,撞击线路EF,第二次反弹线路GH,求证:EF∥GH;
(2)台球经过如图3所示的两次反弹后,撞击线路EF和第二次反弹线路GH是否仍然平行,给出你的结论并说明理由.

分析 (1)由平行线的性质结合题目条件可得∠AFG=∠FGC=∠BFE=∠DGH,则可求得∠GFE=∠HGF,可证明EF∥GH;
(2)结合条件可知∠AFG=∠BFE,∠AGF=∠DGH,由∠A=90°,可求得∠AFG+∠AGF=90°,结合平角的定义可得∠FGH+∠GFE=180°,可证得EF∥GH.
解答 (1)证明:
由题意可知∠AFG=∠BFE,∠DGH=∠CGF,
∵AB∥CD,
∴∠AFG=∠CGF,
∴∠AFG=∠BFE=∠DGH=∠CGF,
∵∠GFE=180°-2∠AFG,∠FGH=180°-2∠CGF,
∴∠GFE=∠FGF,
∴EF∥GH;
(2)解:EF∥GH.理由如下:
由题意可知∠AFG=∠BFE,∠AGF=∠DGH,
∵∠A=90°,
∴∠AFG+∠AGF=90°,
∵∠GFE=180°-2∠AFG,∠FGH=180°-2∠AGF,
∴∠GFE+∠FGH=360°-2(∠AFG+∠AGF)=360°-180°=180°,
∴EF∥GH.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列各数中,是无理数的是( )
| A. | $\sqrt{16}$ | B. | $\sqrt{7}$ | C. | $\frac{3}{11}$ | D. | 3.14 |
15.下列说法正确的是( )
| A. | 若ab=0,则点P(a,b)表示原点 | |
| B. | 点(1,-a2)在第四象限 | |
| C. | 已知点A(2,3)与点B(2,-3),则直线AB平行x轴 | |
| D. | 坐标轴上的点不属于任何象限 |
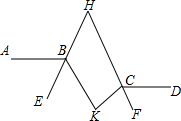 如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=27°,则∠K=78°.
如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=27°,则∠K=78°.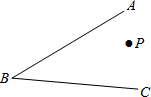 如图,P是∠ABC内一点,
如图,P是∠ABC内一点,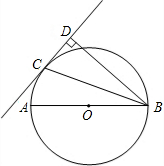 如图,点C是以AB为直径的⊙O上的一点,BD⊥CD,垂足位点D,BC平分∠DBA.
如图,点C是以AB为直径的⊙O上的一点,BD⊥CD,垂足位点D,BC平分∠DBA.