题目内容
20.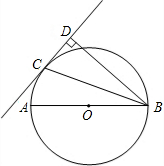 如图,点C是以AB为直径的⊙O上的一点,BD⊥CD,垂足位点D,BC平分∠DBA.
如图,点C是以AB为直径的⊙O上的一点,BD⊥CD,垂足位点D,BC平分∠DBA.(1)求证:CD是⊙O的切线;
(2)若⊙O的半径长为5,BC=8,求:CD的长.
分析 (1)连接OC,由角平分线和等腰三角形的性质得出∠2=∠3,证出OC∥BD,再由BD⊥CD,得出OC⊥CD,即可得出结论;
(2)连接AC,由圆周角定理得出∠BCA=90°,由勾股定理求出AC,证明△ABC∽△CBD,得出对应边成比例$\frac{CD}{AC}=\frac{BC}{AB}$,即可求出CD的长.
解答 (1)证明:连接OC,如图1所示: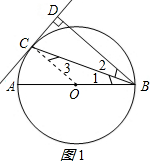
∵BC平分∠DBA,
∴∠1=∠2,
∵OB=OC,
∴∠1=∠3,
∴∠2=∠3,
∴OC∥BD,
∵BD⊥CD,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连接AC,如图2所示: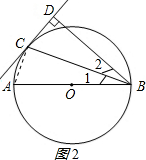 ∵AB为直径,
∵AB为直径,
∴∠BCA=90°,AB=2×5=10,
∴∠BCA=∠BDC=90°,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
又∵∠1=∠2,
∴△ABC∽△CBD,
∴$\frac{CD}{AC}=\frac{BC}{AB}$,
即$\frac{CD}{6}=\frac{8}{10}$,
∴CD=4.8.
点评 本题考查了切线的性质、平行线的判定、圆周角定理、勾股定理、相似三角形的判定与性质;熟练掌握切线的判定方法,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
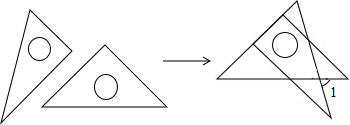

| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
9.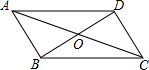 如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
 如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | OA=OC,OB=OD |

 如图,已知双曲线y1=$\frac{k}{x}$经过点D(6,1),点C是双曲线第三象限分支上的动点,过点C作CA⊥x轴,过点D作BD⊥y轴,垂足分别为A,B,连接AB,BC.
如图,已知双曲线y1=$\frac{k}{x}$经过点D(6,1),点C是双曲线第三象限分支上的动点,过点C作CA⊥x轴,过点D作BD⊥y轴,垂足分别为A,B,连接AB,BC.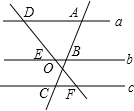 如图,直线a∥b,c∥b,AB=6,BC=3,则$\frac{DE}{DF}$=$\frac{2}{3}$.
如图,直线a∥b,c∥b,AB=6,BC=3,则$\frac{DE}{DF}$=$\frac{2}{3}$.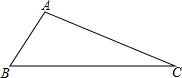 尺规作图,要求:保留作图痕迹,不写作法,不用说明理由.
尺规作图,要求:保留作图痕迹,不写作法,不用说明理由.