题目内容
20.已知点A(1,$\sqrt{3}$),直线y=4x+1沿直线OA方向平移4个单位,平移后的直线解析式为y=4x+2$\sqrt{3}$-7.分析 联立方程组得出点B的坐标,再根据直线y=4x+1沿直线OA方向平移4个单位得出点C的坐标,代入解析式解答即可.
解答 解:如图所示: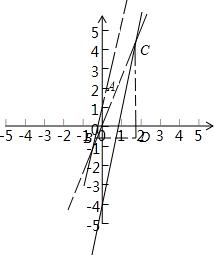
由题意可得直线OP:y=$\sqrt{3}$x,
联立$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{y=4x+1}\end{array}\right.$,
解得:x=-$\frac{\sqrt{3}+4}{13}$,
即点B的横坐标为-$\frac{\sqrt{3}+4}{13}$,
直线y=4x+1沿直线OA方向平移4个单位,即BC=4,
∵${k}_{OP}=\sqrt{3}$,
∴∠ABD=60°,
∴BD=$\frac{1}{2}$BC=2,
∴点C的横坐标为:$\frac{22-\sqrt{3}}{13}$,
将x=$\frac{22-\sqrt{3}}{13}$代入,y=$\sqrt{3}$x得:y=$\frac{22\sqrt{3}-3}{13}$,
∴C($\frac{22-\sqrt{3}}{13},\frac{22\sqrt{3}-3}{13}$),
设平移后的直线解析式为:y=4x+b,
将点C的坐标代入得:$\frac{22\sqrt{3}-3}{13}=4×\frac{22-\sqrt{3}}{13}+b$,
解得:b=$2\sqrt{3}-7$,
所以平移后的直线解析式为:y=4x+2$\sqrt{3}$-7.
故答案为:y=4x+2$\sqrt{3}$-7.
点评 此题考查一次函数与几何变换,关键是根据平移的特点进行分析得出方程组解答.

练习册系列答案
相关题目
8. 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
请结合以上信息解答下列问题.
(1)a=2,本次调查样本的容量是50;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.| 组别 | 捐款额(x)元 | 户数 |
| A | 1≤x<50 | a |
| B | 50≤x<100 | 10 |
| C | 100≤x<150 | |
| D | 150≤x<200 | |
| E | x≥200 |
(1)a=2,本次调查样本的容量是50;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
5.下列等式中正确的是( )
| A. | $\frac{0.1x-0.3y}{0.2x+y}$=$\frac{x-3y}{2x+y}$ | B. | $\frac{x+y}{x-y}$=0 | ||
| C. | $\frac{-x+y}{x-y}$=-1 | D. | $\frac{b}{a}$=$\frac{{b}^{2}}{{a}^{2}}$ |
9.下列为真命题的是( )
| A. | 相等的角是对顶角 | B. | 两点之间线段最短 | ||
| C. | 两直线平行,同旁内角相等 | D. | 若$\sqrt{{a}^{2}}$=a,则a>0 |