题目内容
19.某超市如果将进货价为40元的商品按50元销售,就能卖出500个,但如果这种商品每个涨价1元,其销售量就减少10个,如果你是超市的经理,为了赚得8 000元的利润,你认为售价(售价不能超过进价的160%)应定为多少?这时应进货多少个?分析 根据售价减去进价表示出实际的利润,根据这种商品每个涨价1元,其销售量就减少10个,表示出实际的销售量.由利润=(售价-进价)×销售量,列出方程,求出方程的解即可得到结果.
解答 解:设此商品的单价为(50+x)元,则每个商品的利润是[(50+x)-40]元,销售数量为(500-10x)个.
由题意,得[(50+x)-40](500-10x)=8 000,
整理得x2-40x-300=0.
解得x1=10,x2=30,
∵商品售价不能超过进价的160%,
∴取x=10.
这时应进货500-10x=400(个).
故售价定为60元,这时应进货400个.
点评 此题考查了一元二次方程的应用,解题的关键是理解“商品每个涨价1元,其销售量就减少10个”.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.下列为真命题的是( )
| A. | 相等的角是对顶角 | B. | 两点之间线段最短 | ||
| C. | 两直线平行,同旁内角相等 | D. | 若$\sqrt{{a}^{2}}$=a,则a>0 |
7.为了了解某市八年级8000名学生的体重情况,从中抽查了500名学生的体重进行统计分析,在这个问题中,下列说法正确的是( )
| A. | 8000名学生是总体 | B. | 500名学生是样本 | ||
| C. | 每个学生是个体 | D. | 样本容量是500 |
4.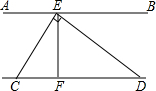 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.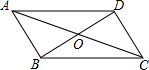 如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
 如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )
如图,在四边形ABCD中,对角线AC于BD相交于点O,下列条件中,不能判定四边形ABCD是平行四边形的是( )| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | OA=OC,OB=OD |

 如图,已知双曲线y1=$\frac{k}{x}$经过点D(6,1),点C是双曲线第三象限分支上的动点,过点C作CA⊥x轴,过点D作BD⊥y轴,垂足分别为A,B,连接AB,BC.
如图,已知双曲线y1=$\frac{k}{x}$经过点D(6,1),点C是双曲线第三象限分支上的动点,过点C作CA⊥x轴,过点D作BD⊥y轴,垂足分别为A,B,连接AB,BC.