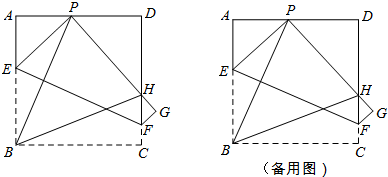
题目内容
1.问题背景:将已知△ABC绕点A逆时针旋转得到△AB′C′,顶点B、C的对应点分别为点B′,C′,连接CC′,且满足CC′∥AB.
探索发现:
(1)若∠BAC=40°,如图1,求旋转角∠CAC′的度数.
(2)若∠BAC=70°,如图2,则旋转角∠CAC′40°
(3)基∠BAC=α,旋转角为β,则β=180°-2α(用含α的代数式表示),其中α=取值范围是0°<α<90°.
应用提升:
(1)将矩形ABCD绕其顶点A逆时针旋转得到矩形AB′C′D′,且点C′落在CD的延长线上.
①当BC=1,AB=$\sqrt{3}$时,旋转角的度数为120°.
②若旋转角度为β(0°<β<180°),∠BAC=α,则α=90°-$\frac{1}{2}β$(用含β的代数式表示).
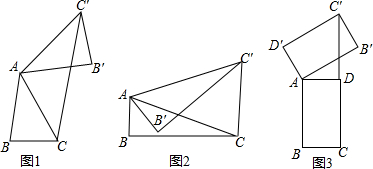
分析 (1)利用旋转的性质和平行线的性质进行计算即可;
(2)利用(1)中的结论解答即可;
(3)利用(1)中的结论得出关系式,进而解出取值范围即可;
应用提升:
(1)①连接AC'和AC,利用旋转的性质和平行线的性质进行计算即可;
②利用①中的结论得出关系式,进而得出代数式即可.
解答 解:(1)如图1: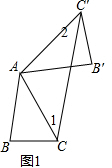
∵AB∥CC',
∴∠1=∠BAC=40°,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=180°-40°-40°=100°;
(2)如图2: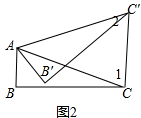
∵AB∥CC',
∴∠1=∠BAC=70°,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=180°-70°-70°=40°;
故答案为:40°;
(3)∵AB∥CC',
∴∠1=∠BAC=α,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=β=180°-α-α=180°-2α,
∴α的取值范围0°<α<90°;
故答案为:180°-2α,0°<α<90°;
应用提升:
(1)①连接AC'和AC,如图3: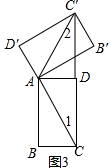
∵矩形ABCD,BC=1,AB=$\sqrt{3}$,
∴∠BAC=30°,
∵AB∥CC',
∴∠1=∠BAC=30°,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=180°-30°-30°=120°;
故答案为:120°;
②∵AB∥CC',
∴∠1=∠BAC=α,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=β=180°-α-α=180°-2α,
所以α=90°-$\frac{1}{2}β$.
故答案为:90°-$\frac{1}{2}β$.
点评 此题考查几何变换问题,关键是根据旋转的性质和平行线的性质进行分析解答.

练习册系列答案
相关题目
9.下列为真命题的是( )
| A. | 相等的角是对顶角 | B. | 两点之间线段最短 | ||
| C. | 两直线平行,同旁内角相等 | D. | 若$\sqrt{{a}^{2}}$=a,则a>0 |
16.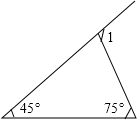 如图,∠1=( )度.
如图,∠1=( )度.
 如图,∠1=( )度.
如图,∠1=( )度.| A. | 110° | B. | 30° | C. | 60° | D. | 120° |