Question

12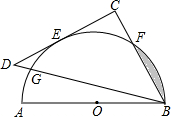．如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．若AB=10cm，则阴影部分面积为（$\frac{25π}{6}$-$\frac{25\sqrt{3}}{4}$）cm²．

Answer 1

分析 连接OE，OF，证明∠ABC=60°，根据阴影部分的面积等于扇形OBF的面积-三角形OBF的面积计算．

解答 解：连接OE，OF，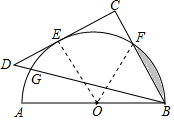
∵CD切半圆O于点E，
∴OE⊥CD，
∵BD为等腰直角△BCD的斜边，
∴BC⊥CD，∠CDB=∠CBD=45°，
∴OE∥BC，
∴∠ABC=∠AOE=60°，
∴△OBF是等边三角形，
∴OF=OB=BF=5cm，
∴S_扇形OBF=$\frac{60π×{5}^{2}}{360}$=$\frac{25π}{6}$（cm²），
S_△OBF=$\frac{1}{2}$×5×$\frac{5\sqrt{3}}{2}$=$\frac{25\sqrt{3}}{4}$（cm²），
∴S_阴影=S_扇形OBF-S_△OBF=（$\frac{25π}{6}$-$\frac{25\sqrt{3}}{4}$）cm²．

点评 本题主要考查扇形面积的计算，把阴影面积转换成求扇形面积和三角形面积是解题的关键．