题目内容
4．分解因式（1）-2x2+18x2y-4xy2
（2）x2（a-1）+x（1-a）
分析 （1）首先找出公因式-2x，进而提取公因式得出答案；
（2）首先提取公因式（a-1），进而利用平方差公式分解因式得出答案．
解答 解：（1）-2x2+18x2y-4xy2
=-2x（x-9y+2y2）；
（2）x2（a-1）+x（1-a）
=x2（a-1）-x（a-1）
=（a-1）（x2-1）
=（a-1）（x+1）（x-1）．
点评 此题主要考查了提取公因式法分解因式以及公式法分解因式，正确提取公因式是解题关键．
练习册系列答案
相关题目
15．
为了解某校七年级学生的身高情况，随机抽取该校男生、女生进行抽样调查，已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
身高情况分组表（单位：cm）
根据图表提供的信息，回答下列问题：
（1）样本中，男生人数为40人，男生身高类别C的组中值为162.5，男生身高类别B的频率为0.3；
（2）样本中，女生身高在E组的人数为2人，女生类别D的频数所对应的扇形圆心角为54°；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？
为了解某校七年级学生的身高情况，随机抽取该校男生、女生进行抽样调查，已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：身高情况分组表（单位：cm）
| 组别 | 身高 |
| A | 145≤x＜155 |
| B | 155≤x＜160 |
| C | 160≤x＜165 |
| D | 165≤x＜170 |
| E | 170≤x＜175 |
（1）样本中，男生人数为40人，男生身高类别C的组中值为162.5，男生身高类别B的频率为0.3；
（2）样本中，女生身高在E组的人数为2人，女生类别D的频数所对应的扇形圆心角为54°；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？
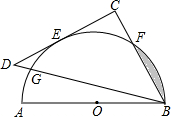如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．若AB=10cm，则阴影部分面积为（$\frac{25π}{6}$-$\frac{25\sqrt{3}}{4}$）cm2．
如图，已知∠BOC=2∠AOB，OD平分∠AOC，∠BOD=14°，求∠AOC的度数．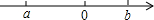
实数a、b在数轴上的位置如图，化简：$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{（a-b）^{2}}$
如图，已知线段AB=4cm．
1．我国是个缺水国家，目前可利用淡水资源总量仅约为899 000乙亿米3，其中数据899 000用科学记数法表示为（ ）
| A． | 8.99×104 | B． | 0.899×106 | C． | 899×103 | D． | 8.99×105 |