题目内容
17．如果三角形的三边a、b、c适合（a2-2ac）（b-a）=c2（a-b），则a、b、c之间满足的关系是a=c≠b；有同学分析后判断△ABC是等边三角形，你的判断是△ABC是等腰三角形．分析 根据已知条件得到a≠b，求得a=c，得到△ABC是等腰三角形，于是得到结论．
解答 解：∵（a2-2ac）（b-a）=c2（a-b），
∴a≠b，
∴a2-2ac=-c2，
∴（a-c）2=0，
∴a=c，
∴△ABC是等腰三角形，
∴a、b、c之间满足的关系是a=c≠b，
故答案为：a=c≠b，△ABC是等腰三角形．
点评 本题考查了等边三角形的判定，熟练掌握等边三角形的判定是解题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
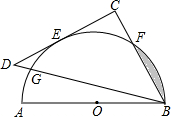如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．若AB=10cm，则阴影部分面积为（$\frac{25π}{6}$-$\frac{25\sqrt{3}}{4}$）cm2．