题目内容
3．先化简，再求值：$\frac{x}{1-x}+\frac{{x}^{2}-6x+9}{{x}^{2}-1}÷\frac{x-3}{x+1}$，其中x取-1、0、1、3中的一个值．分析 原式第二项利用除法法则变形，约分后两项通分并利用同分母分式的加法法则计算得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=-$\frac{x}{x-1}$+$\frac{（x-3）^{2}}{（x+1）（x-1）}$•$\frac{x+1}{x-3}$=-$\frac{x}{x-1}$+$\frac{x-3}{x-1}$=-$\frac{3}{x-1}$，
当x=0时，原式=3．
点评 此题考查了分式的化简求值，熟练掌握分式的加减乘除运算是解本题的关键．
练习册系列答案
相关题目
如图所示，某人从甲地出发，骑摩托车去乙地，途中因车出现故障而停车修理，到达乙地时正好用了2小时，已知摩托车行驶的路程s（千米）与行驶的时间t（时）之间的函数关系由下面的图象OBCD给出，若这辆摩托车平均每行驶100千米的耗油量为2升，则从甲地到乙地，这辆摩托车耗油量为0.9升，车修好后，摩托车的速度为30千米/小时．
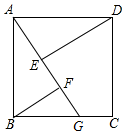在边长为4cm的正方形ABCD中，点G是射线CB上的一点，E、F为直线AG上两个动点，连接DE、BF．