题目内容
8.如图(1),抛物线 y=-$\frac{3}{16}$x2平移后过点A(8,0)和原点,顶点为B,对称轴与x轴相交于点C,与原抛物线相交于点D.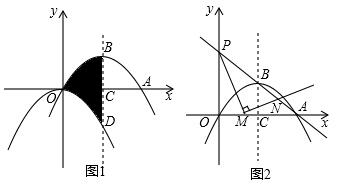
(1)求平移后抛物线的解析式及点D的坐标;
(2)直接写出阴影部分的面积 S阴影;
(3)如图(2),直线AB与y轴相交于点P,点M为线段OA上一动点(点M不与点A,O重合 ),∠PMN为直角,MN与AP相交于点N,设OM=t,试探究:t为何值时,△MAN为等腰三角形?
分析 (1)利用交点式写出平移后的抛物线解析式;
(2)如图1,连接OB、OD,先通过配方法可得到B(4,3),再确定D(4,-3),利用对称性可得到阴影部分的面积 S阴影=S△OBD,然后根据三角形面积公式求解;
(3)先利用待定系数法求出直线AB的解析式为y=-$\frac{3}{4}$x+6,作NQ⊥x轴于Q,如图2,易得P(0,6),AP=10,再证明△MPO∽△NMQ得到$\frac{OM}{NQ}$=$\frac{OP}{MQ}$,然后讨论:当NM=NA时,MQ=AQ=$\frac{1}{2}$(8-t),则OQ=$\frac{1}{2}$t+4,接着利用一次函数图象上点的坐标表示出NQ=-$\frac{3}{8}$t+3,则利用相似比得到$\frac{t}{-\frac{3}{8}t+3}$=$\frac{6}{\frac{1}{2}(8-t)}$,解方程求出满足条件的t的值;当AM=AN时,AN=AM=8-t,证明△ANQ∽△APO,利用相似比可得到NQ=$\frac{3}{5}$(8-t),AQ=$\frac{4}{5}$(8-t),则MQ=8-t-$\frac{4}{5}$(8-t)=$\frac{8-t}{5}$,然后利用相似比得到$\frac{t}{\frac{3}{5}(8-t)}$=$\frac{6}{\frac{8-t}{5}}$,解方程确定满足条件的t的值;当MA=MN时,由于∠OAP<45°,则∠MNA=∠NAM<45°,原式可判断∠AMN>90°,显然不成立,所以当t为$\frac{9}{2}$时,△MAN为等腰三角形.
解答 解:(1)平移后的抛物线解析式为y=-$\frac{3}{16}$x(x-8),
即y=-$\frac{3}{16}$x2+$\frac{3}{2}$x;
(2)如图1,连接OB、OD,
y=-$\frac{3}{16}$(x-4)2+3,则B(4,3)
平移后的抛物线的对称轴为直线x=4,
当x=4时,y=-$\frac{3}{16}$x2=-3,则D(4,-3),
∴点B与点D关于x轴对称,
∴阴影部分的面积 S阴影=S△OBD=$\frac{1}{2}$×3×(4+4)=12;
(3)设直线AB的解析式为y=kx+b,
把A(8,0),B(4,3)代入得$\left\{\begin{array}{l}{8k+b=0}\\{4k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{3}{4}$x+6,
作NQ⊥x轴于Q,如图2,P(0,6),AP=10,
∵∠PMN为直角,
∴∠PMO+∠QMN=90°,
而∠PMO+∠MOP=90°,
∴∠QMN=∠MOP,
∴△MPO∽△NMQ,
∴$\frac{OM}{NQ}$=$\frac{OP}{MQ}$,
当NM=NA时,MQ=AQ=$\frac{1}{2}$(8-t),
∴OQ=8-$\frac{1}{2}$(8-t)=$\frac{1}{2}$t+4,
当x=$\frac{1}{2}$t+4时,y=-$\frac{3}{4}$($\frac{1}{2}$t+4)+6=-$\frac{3}{8}$t+3;
∴$\frac{t}{-\frac{3}{8}t+3}$=$\frac{6}{\frac{1}{2}(8-t)}$,解得t1=8(舍去),t2=$\frac{9}{2}$;
当AM=AN时,AN=AM=8-t,
∵NQ∥OP,
∴△ANQ∽△APO,
∴$\frac{NQ}{OP}$=$\frac{AQ}{AO}$=$\frac{AN}{AP}$,即$\frac{NQ}{6}$=$\frac{AQ}{8}$=$\frac{8-t}{10}$,
∴NQ=$\frac{3}{5}$(8-t),AQ=$\frac{4}{5}$(8-t),
∴MQ=8-t-$\frac{4}{5}$(8-t)=$\frac{8-t}{5}$,
∴$\frac{t}{\frac{3}{5}(8-t)}$=$\frac{6}{\frac{8-t}{5}}$,解得t1=8(舍去),t2=18(舍去;
当MA=MN时,
∵∠OAP<45°,
∴∠MNA=∠NAM<45°,
∴∠AMN>90°,显然不成立,
综上所述,当t为$\frac{9}{2}$时,△MAN为等腰三角形.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的判定;会运用待定系数法求抛物线的解析式;能运用相似比表示线段之间的关系;会应用分类讨论的思想解决数学问题.

 开心快乐假期作业暑假作业西安出版社系列答案
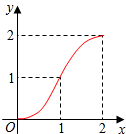
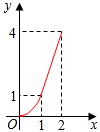
开心快乐假期作业暑假作业西安出版社系列答案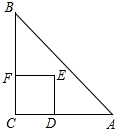 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC上,C、D两点不重合,设CD的长度为x,Rt△ABC与正方形CDEF重叠部分的面积为y,则下列中能表示y与x之间的关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC上,C、D两点不重合,设CD的长度为x,Rt△ABC与正方形CDEF重叠部分的面积为y,则下列中能表示y与x之间的关系的是( )
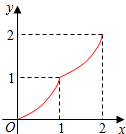
 二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.
二次函数y=$\frac{2}{3}$x2的函数图象如图,点A0位于坐标原点,点A1,A2,A3…A10 在y轴的正半轴上,点B1,B2,B3…B10在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都为等边三角形,则△A9B10A10的边长为10.