题目内容
 如图,已知抛物线y=-
如图,已知抛物线y=-| 3 |
| 4 |
| 3 |
| 4t |
(1)确定b,c的值:b=
(2)写出B,Q,P的坐标,(其中Q,P用含t的式子表示)
B(
(3)依点P的变化,是否存在t的值,使△PQB是等腰三角形?若存在,求出所有t值;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)将A、C的坐标代入抛物线中即可求得待定系数的值.
(2)根据抛物线的解析式可求得B点的坐标,即可求出OB,BC的长,在直角三角形BPH中,可根据BP的长和∠CBO三角函数求出PH,BH的长,进而可求出OH的长,也就求出了P点的坐标.Q点的坐标,可直接由直线CQ的解析式求得.
(3)本题要分情况讨论:
①PQ=PB,此时BH=QH=
BQ,在(2)中已经求得了BH的长,BQ的长可根据B、Q点的坐标求得,据此可求出t的值.
②PB=BQ,那么BQ=BP=5t,由此可求出t的值.
③PQ=BQ,已经求得了BH的长,可表示出QH的长,然后在Rt△PQH中,用BQ的表达式表示出PQ,即可用勾股定理求出t的值.
(2)根据抛物线的解析式可求得B点的坐标,即可求出OB,BC的长,在直角三角形BPH中,可根据BP的长和∠CBO三角函数求出PH,BH的长,进而可求出OH的长,也就求出了P点的坐标.Q点的坐标,可直接由直线CQ的解析式求得.
(3)本题要分情况讨论:
①PQ=PB,此时BH=QH=
| 1 |
| 2 |
②PB=BQ,那么BQ=BP=5t,由此可求出t的值.
③PQ=BQ,已经求得了BH的长,可表示出QH的长,然后在Rt△PQH中,用BQ的表达式表示出PQ,即可用勾股定理求出t的值.
解答:解:(1)已知抛物线过A(-1,0)、C(0,3),则有:
,
解得
.
因此b=
,c=3.
故答案为:
,3;
(2)令抛物线的解析式中y=0,则有-
x2+
x+3=0,
解得:x1=-1,x2=4;
故B(4,0),OB=4,
因此BC=5,
在直角三角形OBC中,OB=4,OC=3,BC=5,
则sin∠CBO=
,cos∠CBO=
,
在Rt△BHP中,BP=5t,
因此PH=3t,BH=4t;
则OH=OB-BH=4-4t,
因此P(4-4t,3t).
令直线的解析式中y=0,则有0=-
x+3,解得:x=4t,
故Q(4t,0).
故答案为:(4,0),(4t,0),(4-4t,3t);
(3)存在t的值,有以下三种情况
①如图1,当PQ=PB时,
∵PH⊥OB,则QH=HB,
∴4-4t-4t=4t,
∴解得:t=
,
②如图2,当PB=QB得4-4t=5t,
∴解得:t=
,
③如图3,当PQ=QB时,在Rt△PHQ中有QH2+PH2=PQ2,
∴(8t-4)2+(3t)2=(4-4t)2,
∴57t2-32t=0,
∴解得:t=
,t=0(舍去),
又∵0<t<1,
∴当t=
或
或
时,△PQB为等腰三角形.
|
解得
|
因此b=
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
(2)令抛物线的解析式中y=0,则有-
| 3 |
| 4 |
| 9 |
| 4 |
解得:x1=-1,x2=4;

故B(4,0),OB=4,
因此BC=5,
在直角三角形OBC中,OB=4,OC=3,BC=5,
则sin∠CBO=
| 3 |
| 5 |
| 4 |
| 5 |
在Rt△BHP中,BP=5t,
因此PH=3t,BH=4t;
则OH=OB-BH=4-4t,
因此P(4-4t,3t).
令直线的解析式中y=0,则有0=-
| 3 |
| 4t |
故Q(4t,0).

故答案为:(4,0),(4t,0),(4-4t,3t);
(3)存在t的值,有以下三种情况
①如图1,当PQ=PB时,
∵PH⊥OB,则QH=HB,
∴4-4t-4t=4t,
∴解得:t=
| 1 |
| 3 |
②如图2,当PB=QB得4-4t=5t,

∴解得:t=
| 4 |
| 9 |
③如图3,当PQ=QB时,在Rt△PHQ中有QH2+PH2=PQ2,
∴(8t-4)2+(3t)2=(4-4t)2,
∴57t2-32t=0,
∴解得:t=
| 32 |
| 57 |
又∵0<t<1,
∴当t=
| 1 |
| 3 |
| 4 |
| 9 |
| 32 |
| 57 |
点评:本题考查了二次函数的确定以及等腰三角形的判定等知识点.要注意的是(3)题中在不确定等腰三角形的腰和底的情况下腰分类讨论,不要漏解.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O且MN∥BC,若AB=12,AC=18,求△AMN的周长.
如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O且MN∥BC,若AB=12,AC=18,求△AMN的周长. 某木工师傅制作如图的一个工件(阴影部分).
某木工师傅制作如图的一个工件(阴影部分).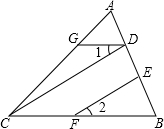 已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF平行吗?为什么?
已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF平行吗?为什么? 如图,△ABC为等腰直角三角形,∠C=90°,AC=6.动点O在△ABC的边上,从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、半径为1的圆在运动过程中与△ABC的边BC相切时是出发后第
如图,△ABC为等腰直角三角形,∠C=90°,AC=6.动点O在△ABC的边上,从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、半径为1的圆在运动过程中与△ABC的边BC相切时是出发后第