题目内容
把下列各式分解因式:
(1)3(a-b)x2-15(a-b)xy+18(b-a)y2;
(2)-x5y+81xy;
(3)(x2+64)2-256x2;
(4)a2-b2-1-2b;
(5)30a3-10a2x+6a2y-2axy;
(6)(x2-2x-5)(x2-2x+4)+14.
(1)3(a-b)x2-15(a-b)xy+18(b-a)y2;
(2)-x5y+81xy;
(3)(x2+64)2-256x2;
(4)a2-b2-1-2b;
(5)30a3-10a2x+6a2y-2axy;
(6)(x2-2x-5)(x2-2x+4)+14.
考点:整式的混合运算
专题:计算题
分析:(1)原式提取公因式后,利用十字相乘法分解即可;
(2)原式提取公因式后,利用平方差公式分解即可;
(3)原式利用平方差公式化简,再利用完全平方公式分解即可;
(4)原式后三项结合后,利用完全平方公式化简,再利用平方差公式分解即可;
(5)原式提取公因式即可得到结果;
(6)原式变形后,利用十字相乘法分解即可.
(2)原式提取公因式后,利用平方差公式分解即可;
(3)原式利用平方差公式化简,再利用完全平方公式分解即可;
(4)原式后三项结合后,利用完全平方公式化简,再利用平方差公式分解即可;
(5)原式提取公因式即可得到结果;
(6)原式变形后,利用十字相乘法分解即可.
解答:解:(1)原式=3(a-b)(x2-5xy+6y2)=3(a-b)(x-2y)(x-3y);
(2)原式=xy(81-x4)=xy(9+x2)(9-x2)=xy(9+x2)(3+x)(3-x);
(3)原式=(x2+64-16x)(x2+64+16x)=(x-8)2(x+8)2;
(4)原式=a2-(b+1)2=(a+b+1)(a-b-1);
(5)原式=a(30a2-10ax+6ay-2xy);
(6)原式=(x2-2x)2-(x2-2x)-6=(x2-2x-3)(x2-2x+2)=(x-3)(x+1)(x2-2x+2).
(2)原式=xy(81-x4)=xy(9+x2)(9-x2)=xy(9+x2)(3+x)(3-x);
(3)原式=(x2+64-16x)(x2+64+16x)=(x-8)2(x+8)2;
(4)原式=a2-(b+1)2=(a+b+1)(a-b-1);
(5)原式=a(30a2-10ax+6ay-2xy);
(6)原式=(x2-2x)2-(x2-2x)-6=(x2-2x-3)(x2-2x+2)=(x-3)(x+1)(x2-2x+2).
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
A、
| ||||
B、
| ||||
| C、-5x2的系数为5 | ||||
| D、-x2的系数为1 |
 如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.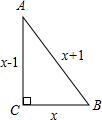 阅读:
阅读: 如图,已知抛物线y=-
如图,已知抛物线y=-