题目内容
 如图,△ABC为等腰直角三角形,∠C=90°,AC=6.动点O在△ABC的边上,从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、半径为1的圆在运动过程中与△ABC的边BC相切时是出发后第
如图,△ABC为等腰直角三角形,∠C=90°,AC=6.动点O在△ABC的边上,从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、半径为1的圆在运动过程中与△ABC的边BC相切时是出发后第考点:轨迹
专题:
分析:当O在AC上时,O为圆心、半径为1的圆与BC相切,求得OC的长即可;
当O在AB上时,设为O',设圆与BC的切点是D,连接O'D.易证△O'DB是等腰直角三角形,求得O'D的长,即可求解.
当O在AB上时,设为O',设圆与BC的切点是D,连接O'D.易证△O'DB是等腰直角三角形,求得O'D的长,即可求解.
解答: 解:当O在AC上时,O为圆心、半径为1的圆与BC相切,则OC=1,则AO=6-1=5,即出发5秒后与BC相切;
解:当O在AC上时,O为圆心、半径为1的圆与BC相切,则OC=1,则AO=6-1=5,即出发5秒后与BC相切;
当O在AB上时,设为O',设圆与BC的切点是D,连接O'D.
∵⊙O'和BC相切,
∴O'D⊥BC,
又∵△ABC是等腰直角三角形,
∴∠B=45°,
∴△O'BD是等腰直角三角形,且O'D=BD=1,
∴O'B=
=
.
则AC+BC+O'B=12+
.
故出发后第5和12+
秒圆和BC相切.
故答案是:5和12+
.
 解:当O在AC上时,O为圆心、半径为1的圆与BC相切,则OC=1,则AO=6-1=5,即出发5秒后与BC相切;
解:当O在AC上时,O为圆心、半径为1的圆与BC相切,则OC=1,则AO=6-1=5,即出发5秒后与BC相切;当O在AB上时,设为O',设圆与BC的切点是D,连接O'D.
∵⊙O'和BC相切,
∴O'D⊥BC,
又∵△ABC是等腰直角三角形,
∴∠B=45°,
∴△O'BD是等腰直角三角形,且O'D=BD=1,
∴O'B=
| 12+12 |
| 2 |
则AC+BC+O'B=12+
| 2 |
故出发后第5和12+
| 2 |
故答案是:5和12+
| 2 |
点评:本题考查了切线的性质,注意到△O'DB是等腰直角三角形是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,已知抛物线y=-
如图,已知抛物线y=-
 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=2,则DE的值为
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=2,则DE的值为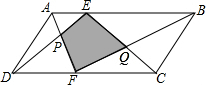 如图,E、F是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15cm2,S△BOC=25cm2,则阴影部分的面积为
如图,E、F是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15cm2,S△BOC=25cm2,则阴影部分的面积为