题目内容
6．已知$\frac{{x}^{2}+2x+1}{（x-2）^{3}}$=$\frac{A}{x-2}$+$\frac{B}{（x-2）^{2}}$+$\frac{C}{（x-2）^{3}}$，求A、B、C的值．分析 先通分右边，再进行分式的加法，根据对应相等的原则即可得出A、B、C的值．
解答 解：右边=$\frac{A（x-2）^{2}}{（x-2）^{3}}$+$\frac{B（x-2）}{（x-2）^{3}}$+$\frac{C}{（x-2）^{3}}$
=$\frac{A{x}^{2}-4Ax+4A+Bx-2B+C}{（x-2）^{3}}$
=$\frac{A{x}^{2}+（B-4A）x+4A-2B+C}{（x-2）^{3}}$，
∵左边=$\frac{{x}^{2}+2x+1}{（x-2）^{3}}$，
∴$\left\{\begin{array}{l}{A=1}\\{B-4A=2}\\{4A-2B+C=1}\end{array}\right.$，
解得$\left\{\begin{array}{l}{A=1}\\{B=6}\\{C=9}\end{array}\right.$，
答：A、B、C的值分别为1，6，9．
点评 本题考查了分式的加减法，以及解方程组，分式的通分是解题的关键．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
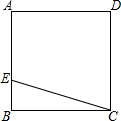如图，ABCD是一块正方形的场地，小华和小芳在AB边上选定了一点E，测量知EC=30m，EB=10m，这块场地的面积和对角线长分别是多少？
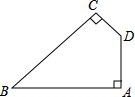如图，在四边形ABCD中，∠A=∠C=90°，∠B=45°．AB=2$\sqrt{7}$，CD=$\sqrt{5}$，求四边形ABCD的面积．
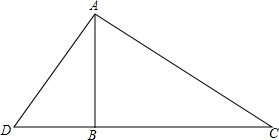如图所示，一棵32米高的巨大杉树在海棠号台风中被刮断，树顶C落在离树根B点16米处，科研人员要看查看断痕A处的情况，在离树根B有5米的D处竖起一个梯子AD，请问这个梯子有多长？
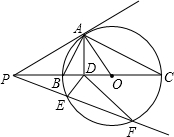如图，△ABC内接于⊙O，BC是⊙O的直径，AD⊥BC，D为垂足，BD＜DC，过点A的切线交直径CB的延长线于点P，过点P任作⊙O的割线PEF交⊙O于点E、F，已知AB=2，$\frac{BD}{DC}+\frac{DC}{BD}=\frac{10}{3}$