题目内容
18．已知m2+n2=3，x2+y2=671，求多项式（mx+ny）2+（nx-my）2的值．分析 先根据完全平方公式展开，再合并后分解因式，最后整体代入求出即可．
解答 解：∵m2+n2=3，x2+y2=671，
∴（mx+ny）2+（nx-my）2
=m2x2+2mnxy+n2y2+n2x2-2mnxy+m2y2
=（m2+n2）x2+（m2+n2）y2
=（m2+n2）（x2+y2）
=3×671
=2013．
点评 本题考查了整式的混合运算和求值，分解因式的应用，能求出原式=（m2+n2）（x2+y2）是解此题的关键，用了整体代入思想，难度适中．
练习册系列答案
相关题目
9．
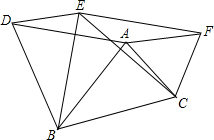如图，在△ABC中，AB=4，AC=3，BC=5，以三边为边，在BC的同侧分别作三个等边三角形即△ABD，△BCE，△ACF．
（1）求证：四边形EFAD是平行四边形；
（2）求四边形EFAD的面积．
如图，在△ABC中，AB=4，AC=3，BC=5，以三边为边，在BC的同侧分别作三个等边三角形即△ABD，△BCE，△ACF．（1）求证：四边形EFAD是平行四边形；
（2）求四边形EFAD的面积．
13．如下表，方程1、方程2、方程3…是按照一定的规律排列的一列方程，解方程3，并将它的解填在表中的空白处．
（1）请写出这列方程中第m个方程，并写出它的解．
（2）用你探究的规律解方程x2-8x-20=0．
| 序号 | 方程 | 方程的解 | |
| 1 | x2+2x-3=0 | x1=1 | x2=-3 |
| 2 | x2+4x-12=0 | x1=2 | x2=-6 |
| 3 | x2+6x-27=0 | x1=3 | x2=-9 |
| … | … | … | … |
（2）用你探究的规律解方程x2-8x-20=0．
