题目内容
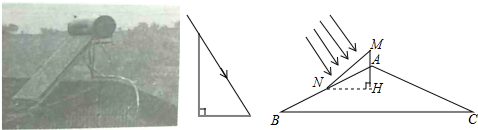
16.如图,AB垂直平分CD,AB与CD相交于点O,CD=4cm,∠CAD=90°,∠CBD=60°,点P、Q、M、N分别沿图示方向在线段上运动,同时开始以1cm/s的速度运动.(1)设出发时间为t(s)是否存在某一时刻,四边形PQMN为既为轴对称图形,又为中心对称图形?若存在,请证明时间;若不存在,请说明理由;
(2)点P、Q、M、N分别与点O连结,图中阴影部分图形称为蝶形,求蝶形面积S关于t的函数关系式(0<t<
(3)当t=2时,在AB上找一点G,使GQ+GM最小,画出图形并求此时OG的长.
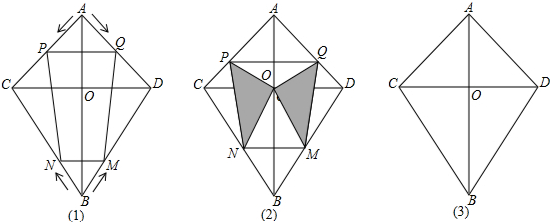
分析 (1)根据线段垂直平分线的性质得CO=DO,AC=AD,再由∠CAD=90°,∠CBD=60°,CD=4,AP=AQ=BM=BN=t,易判断△APG和△ACD为等腰直角三角形,△BMN和△BCD为等边三角形,所以AO=CO=DO=1,BO=2$\sqrt{3}$,CB=DB=4,PQ=$\sqrt{2}$t,MN=t,然后利用PQ∥MN,PM=QN得到四边形PQMN为矩形,当PQ=MN时,四边形PQMN为长方形,则$\sqrt{2}$t=t,解得t=0,于是得到不存在某一时刻,四边形PQMN为既为轴对称图形,又为中心对称图形;
(2)如图(2),AB与PQ、MN交于点E、F,根据等腰直角三角形和等边三角形的性质由PQ=$\sqrt{2}$t,MN=t得到AE=$\frac{1}{2}$PQ=$\frac{\sqrt{2}}{2}$t,BF=$\frac{\sqrt{3}}{2}$MN=$\frac{\sqrt{3}}{2}$t,得到OE=OA-AE=2-$\frac{\sqrt{2}}{2}$t,OF=OB-BF=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t,求得S=-$\frac{2+\sqrt{2}}{4}$t2+(1+$\sqrt{6}$)t;
(3)当t=$\sqrt{2}$时,PQ=2,MN=$\sqrt{2}$,即点Q与D重合,如图(3),连接NQ交AB于G点,由于M关于AB的对称点为N,则GN=GM,所以GQ+GM=GN+GQ=NQ,根据两点之间线段最短得到此时G点使GQ+GM最小,建立如图(3)的直角坐标系,则D(2,0),再确定N点坐标,然后利用待定系数法求出直线NQ的解析式,接着确定G点坐标,于是可得到OG的长.
解答  解:(1)∵AB垂直平分CD,
解:(1)∵AB垂直平分CD,
∴CO=DO,AC=AD,
∵∠CAD=90°,∠CBD=60°,CD=4,AP=AQ=BM=BN=t
∴△APG和△ACD为等腰直角三角形,△BMN和△BCD为等边三角形,
∴AO=CO=DO=2,BO=2$\sqrt{3}$,CB=DB=2,PQ=$\sqrt{2}$t,MN=t,
∵PQ∥CD,MN∥CD,
∴PQ∥MN,且PM=NQ,
∴当PQ=MN时,四边形PQMN为中心对称图形,则$\sqrt{2}$t=t,解得t=0,
∴不存在某一时刻,四边形PQMN既为轴对称图形,又为中心对称图形;
(2)如图(2),AB与PQ、MN交于点E、F,
∵PQ=$\sqrt{2}$t,MN=t,
∴AE=$\frac{1}{2}$PQ=$\frac{\sqrt{2}}{2}$t,BF=$\frac{\sqrt{3}}{2}$MN=$\frac{\sqrt{3}}{2}$t,
∴OE=OA-AE=2-$\frac{\sqrt{2}}{2}$t,OF=OB-BF=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t,
S=S梯形PQMN-S△POQ-S△MON
=$\frac{1}{2}$(t+$\sqrt{2}$t)•(2-$\frac{\sqrt{2}}{2}$t+2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t)-$\frac{1}{2}•$$\sqrt{2}$t•(2-$\frac{\sqrt{2}}{2}$t)-$\frac{1}{2}$t•(2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t),
∴S=-$\frac{2+\sqrt{2}}{4}$t2+(1+$\sqrt{6}$)t; 如图(3),连接NQ交AB于G点,
如图(3),连接NQ交AB于G点,
∵M关于AB的对称点为N,
∴GN=GM,
∴GQ+GM=GN+GQ=NQ,
∴此时G点使GQ+GM最小,
建立如图3所示的直角坐标系,则D(2,0),
∵OF=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t=$\sqrt{3}$,NF=$\frac{1}{2}$MN=1,
∴N(-1,-$\sqrt{3}$)
设直线NQ的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-\sqrt{3}=-k+b}\\{0=2k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$
∴G(0,-$\frac{2\sqrt{3}}{3}$)
∴OG=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了四边形的综合题:熟练掌握线段的垂直平分线的性质、矩形的判定方法、等腰直角三角形和等边三角形的性质;会利用面积的和差计算不规则图形的面积;能利用两点之间线段最短解决两线段和的最小值问题;学会运用函数思想解决数学问题.

 阅读快车系列答案
阅读快车系列答案| A. | 某种彩票的中奖率为1%,买100张彩票也可能没有1张的是中奖 | |
| B. | 从装有10个红球的袋子中,摸出1个白球是不可能事件 | |
| C. | 陨石落在地球上,它会落入海洋的概率是$\frac{1}{2}$ | |
| D. | 在13位同学中,一定有2位同学的出生月份是相同的 |
 如图,AB∥CD,∠1=112°,则∠C=68°.
如图,AB∥CD,∠1=112°,则∠C=68°. 如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动,运动到点A停止,同时一动点Q从点D出发,以每秒3个单位长度的速度沿DC向点C运动,与点P同时停止,设点P运动的时间为t秒.
如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从B点出发沿BA向点A运动,运动到点A停止,同时一动点Q从点D出发,以每秒3个单位长度的速度沿DC向点C运动,与点P同时停止,设点P运动的时间为t秒.