题目内容
8.问题提出(1)如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
问题探究
(2)如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决
(3)如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=$\sqrt{5}$ 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.

分析 (1)作B关于AC 的对称点D,连接AD,CD,△ACD即为所求;
(2)作E关于CD的对称点E′,作F关于BC的对称点F′,连接E′F′,得到此时四边形EFGH的周长最小,根据轴对称的性质得到BF′=BF=AF=2,DE′=DE=2,∠A=90°,于是得到AF′=6,AE′=8,求出E′F′=10,EF=2$\sqrt{5}$即可得到结论;
(3)根据余角的性质得到1=∠2,推出△AEF≌△BGF,根据全等三角形的性质得到AF=BG,AE=BF,设AF=x,则AE=BF=3-x根据勾股定理列方程得到AF=BG=1,BF=AE=2,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°,以O为圆心,以EG为半径作⊙O,则∠EHG=45°的点H在⊙O上,连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′GH′,则∠EH′G=45°,于是得到四边形EFGH′是符合条件的最大部件,根据矩形的面积公式即可得到结论.
解答  解:(1)如图1,△ADC即为所求;
解:(1)如图1,△ADC即为所求;
(2)存在,理由:作E关于CD的对称点E′,
作F关于BC的对称点F′,
连接E′F′,交BC于G,交CD于H,连接FG,EH,
则F′G=FG,E′H=EH,则此时四边形EFGH的周长最小,
由题意得:BF′=BF=AF=2,DE′=DE=2,∠A=90°,
∴AF′=6,AE′=8,
∴E′F′=10,EF=2$\sqrt{5}$,
∴四边形EFGH的周长的最小值=EF+FG+GH+HE=EF+E′F′=2$\sqrt{5}$+10,
∴在边BC、CD上分别存在点G、H,
使得四边形EFGH的周长最小,
最小值为2$\sqrt{5}$+10;
(3)能裁得,
理由:∵EF=FG=$\sqrt{5}$,∠A=∠B=90°,∠1+∠AFE=∠2+AFE=90°,
∴∠1=∠2,
在△AEF与△BGF中,$\left\{\begin{array}{l}{∠1=∠2}\\{∠A=∠B}\\{EF=FG}\end{array}\right.$,
∴△AEF≌△BGF,
∴AF=BG,AE=BF,设AF=x,则AE=BF=3-x,
∴x2+(3-x)2=($\sqrt{5}$)2,解得:x=1,x=2(不合题意,舍去),
∴AF=BG=1,BF=AE=2,
∴DE=4,CG=5,
连接EG,
作△EFG关于EG的对称△EOG,
则四边形EFGO是正方形,∠EOG=90°,
以O为圆心,以OE为半径作⊙O,
∵CE=CG=5,
则∠EHG=45°的点在⊙O上,
连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,
连接EH′、GH′,则∠EH′G=45°,
此时,四边形EFGH′是要想裁得符合要求的面积最大的,
∴C在线段EG的垂直平分线上,
∴点F,O,H′,C在一条直线上,
∵EG=$\sqrt{10}$,
∴OF=EG=$\sqrt{10}$,
∵CF=2$\sqrt{10}$,
∴OC=$\sqrt{10}$,
∵OH′=OE=FG=$\sqrt{5}$,
∴OH′<OC,
∴点H′在矩形ABCD的内部,
∴可以在矩形ABCD中,裁得符合条件的面积最大的四边形EFGH′部件,
这个部件的面积=$\frac{1}{2}$EG•FH′=$\frac{1}{2}$×$\sqrt{10}$×($\sqrt{10}$+$\sqrt{5}$)=5+$\frac{5\sqrt{2}}{2}$,
∴当所裁得的四边形部件为四边形EFGH′时,裁得了符合条件的最大部件,这个部件的面积为(5+$\frac{5\sqrt{2}}{2}$)m2.
点评 本题考查了全等三角形的判定和性质,矩形的性质,勾股定理,轴对称的性质,存在性问题,掌握的作出辅助线利用对称的性质解决问题是解题的关键.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案 如图,AE∥DF,AE=DF.则添加下列条件还不能使△EAC≌△FDB.( )
如图,AE∥DF,AE=DF.则添加下列条件还不能使△EAC≌△FDB.( )| A. | AB=CD | B. | CE∥BF | C. | CE=BF | D. | ∠E=∠F |
| 销售单价x(元/kg) | 120 | 130 | … | 180 |
| 每天销量y(kg) | 100 | 95 | … | 70 |
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
 在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:“宇番2号”番茄挂果数量统计表
| 挂果数量x(个) | 频数(株) | 频率 |
| 25≤x<35 | 6 | 0.1 |
| 35≤x<45 | 12 | 0.2 |
| 45≤x<55 | a | 0.25 |
| 55≤x<65 | 18 | b |
| 65≤x<75 | 9 | 0.15 |
(1)统计表中,a=15,b=0.3;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为72°;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有300株.
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
 如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )
如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )| A. | 85° | B. | 60° | C. | 50° | D. | 35° |
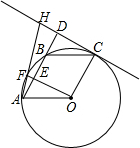 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H. 已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.
已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD. 某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人
某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人