题目内容
7. 平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)在(1)的条件下,若△APO的面积为2,求点D到直线AC的距离.
分析 (1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;
(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据点到直线的距离公式可以求得点D到直线AC的距离.
解答  解:(1)∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
解:(1)∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y=$\frac{k}{x}$(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
∴3=$\frac{k}{2}$,点C与点A关于原点O对称,
∴k=6,C(-2,-3),
即k的值是6,C点的坐标是(-2,-3);
(2)过点A作AN⊥y轴于点N,过点D作DM⊥AC,如图,
∵点A(2,3),k=6,
∴AN=2,
∵△APO的面积为2,
∴$\frac{OP•AN}{2}=2$,
即$\frac{OP•2}{2}=2$,得OP=2,
∴点P(0,2),
设过点A(2,3),P(0,2)的直线解析式为y=kx+b,
$\left\{\begin{array}{l}{2k+b=3}\\{b=2}\end{array}\right.$,得$\left\{\begin{array}{l}{k=0.5}\\{b=2}\end{array}\right.$,
∴过点A(2,3),P(0,2)的直线解析式为y=0.5x+2,
当y=0时,0=0.5x+2,得x=-4,
∴点D的坐标为(-4,0),
设过点A(2,3),B(-2,-3)的直线解析式为y=mx+b,
则$\left\{\begin{array}{l}{2m+n=3}\\{-2m+n=-3}\end{array}\right.$,得$\left\{\begin{array}{l}{m=1.5}\\{n=0}\end{array}\right.$,
∴过点A(2,3),C(-2,-3)的直线解析式为y=1.5x,
∴点D到直线AC的直线得距离为:$\frac{|1.5×(-4)-0|}{\sqrt{1.{5}^{2}+(-1)^{2}}}$=$\frac{12\sqrt{13}}{13}$.
点评 本题考查反比例函数与一次函数的交点问题、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

 53随堂测系列答案
53随堂测系列答案 如图,AE∥DF,AE=DF.则添加下列条件还不能使△EAC≌△FDB.( )
如图,AE∥DF,AE=DF.则添加下列条件还不能使△EAC≌△FDB.( )| A. | AB=CD | B. | CE∥BF | C. | CE=BF | D. | ∠E=∠F |
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | 3$\sqrt{3}$×2$\sqrt{2}$=6$\sqrt{5}$ | C. | 3$\sqrt{5}$÷$\frac{1}{{\sqrt{3}}}$×$\sqrt{3}$=3$\sqrt{5}$ | D. | 3÷$\sqrt{\frac{2}{3}}$=$\frac{3}{2}\sqrt{6}$ |
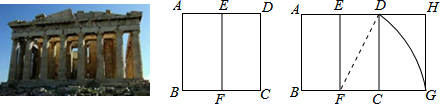
| A. | 矩形ABFE | B. | 矩形EFCD | C. | 矩形EFGH | D. | 矩形DCGH |
| 销售单价x(元/kg) | 120 | 130 | … | 180 |
| 每天销量y(kg) | 100 | 95 | … | 70 |
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
 在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:“宇番2号”番茄挂果数量统计表
| 挂果数量x(个) | 频数(株) | 频率 |
| 25≤x<35 | 6 | 0.1 |
| 35≤x<45 | 12 | 0.2 |
| 45≤x<55 | a | 0.25 |
| 55≤x<65 | 18 | b |
| 65≤x<75 | 9 | 0.15 |
(1)统计表中,a=15,b=0.3;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为72°;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有300株.
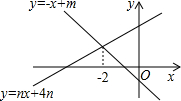 如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( )
如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n>0的整数解为( ) 已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.
已知:如图,⊙O是△ABC的外接圆,$\widehat{AB}$=$\widehat{AC}$,点D在边BC上,AE∥BC,AE=BD.