题目内容
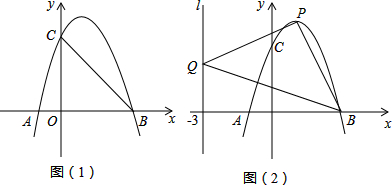
11.如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=-3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
分析 (1)利用待定系数法求出抛物线的解析式即可;
(2)先求出直线BC解析式为y=-x+3,再求出抛物线顶点坐标,得出当x=1时,y=2;结合抛物线顶点坐即可得出结果;
(3)设P(m,-m2+2m+3),Q(-3,n),由勾股定理得出PB2=(m-3)2+(-m2+2m+3)2,PQ2=(m+3)2+(-m2+2m+3-n)2,BQ2=n2+36,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,由AAS证明△PQM≌△BPN,得出MQ=NP,PM=BN,则MQ=-m2+2m+3-n,PN=3-m,得出方程-m2+2m+3-n=3-m,解方程即可.
解答 解:(1)∵抛物线的对称轴x=1,B(3,0),
∴A(-1,0)
∵抛物线y=ax2+bx+c过点C(0,3)
∴当x=0时,c=3.
又∵抛物线y=ax2+bx+c过点A(-1,0),B(3,0)
∴$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$
∴抛物线的解析式为:y=-x2+2x+3;
(2)∵C(0,3),B(3,0),
∴直线BC解析式为y=-x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标为(1,4)
∵对于直线BC:y=-x+1,当x=1时,y=2;将抛物线L向下平移h个单位长度,
∴当h=2时,抛物线顶点落在BC上;
当h=4时,抛物线顶点落在OB上,
∴将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),
则2≤h≤4;
(3)设P(m,-m2+2m+3),Q(-3,n),
①当P点在x轴上方时,过P点作PM垂直于y轴,交y轴与M点,过B点作BN垂直于MP的延长线于N点,如图所示:
∵B(3,0),
∵△PBQ是以点P为直角顶点的等腰直角三角形,
∴∠BPQ=90°,BP=PQ,
则∠PMQ=∠BNP=90°,∠MPQ=∠NBP,
在△PQM和△BPN中,$\left\{\begin{array}{l}{∠PMQ=∠BNP}&{\;}\\{∠MPQ=∠NBP}&{\;}\\{PQ=BP}&{\;}\end{array}\right.$,
∴△PQM≌△BPN(AAS),
∴PM=BN,
∵PM=BN=-m2+2m+3,根据B点坐标可得PN=3-m,且PM+PN=6,
∴-m2+2m+3+3-m=6,
解得:m=1或m=0,
∴P(1,4)或P(0,3).
②当P点在x轴下方时,过P点作PM垂直于l于M点,过B点作BN垂直于MP的延长线于N点,
同理可得△PQM≌△BPN,
∴PM=BN,
∴PM=6-(3-m)=3+m,BN=m2-2m-3,
则3+m=m2-2m-3,
解得m=$\frac{3+\sqrt{33}}{2}$或$\frac{3-\sqrt{33}}{2}$.
∴P($\frac{3+\sqrt{33}}{2}$,$\frac{-\sqrt{33}-9}{2}$)或($\frac{3-\sqrt{33}}{2}$,$\frac{\sqrt{33}-9}{2}$).
综上可得,符合条件的点P的坐标是(1,4),(0,3),($\frac{3+\sqrt{33}}{2}$,$\frac{-\sqrt{33}-9}{2}$)和($\frac{3-\sqrt{33}}{2}$,$\frac{\sqrt{33}-9}{2}$).
点评 本题是二次函数综合题目,考查了用待定系数法求出抛物线的解析式、抛物线的顶点式、等腰直角三角形的性质、全等三角形的判定与性质、坐标与图形性质等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线证明三角形全等才能得出结果.

| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | 3$\sqrt{3}$×2$\sqrt{2}$=6$\sqrt{5}$ | C. | 3$\sqrt{5}$÷$\frac{1}{{\sqrt{3}}}$×$\sqrt{3}$=3$\sqrt{5}$ | D. | 3÷$\sqrt{\frac{2}{3}}$=$\frac{3}{2}\sqrt{6}$ |
| 销售单价x(元/kg) | 120 | 130 | … | 180 |
| 每天销量y(kg) | 100 | 95 | … | 70 |
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
 在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:“宇番2号”番茄挂果数量统计表
| 挂果数量x(个) | 频数(株) | 频率 |
| 25≤x<35 | 6 | 0.1 |
| 35≤x<45 | 12 | 0.2 |
| 45≤x<55 | a | 0.25 |
| 55≤x<65 | 18 | b |
| 65≤x<75 | 9 | 0.15 |
(1)统计表中,a=15,b=0.3;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为72°;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有300株.
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |

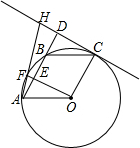 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H.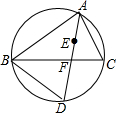 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D