题目内容
已知等腰梯形下底长4厘米，高是2厘米，下底的内角的正弦值是
，则上底长为 厘米．
| 4 |
| 5 |
考点：等腰梯形的性质,解直角三角形
专题：
分析：根据题意，作出图形，根据下底的内角的正弦值是
，高为2cm，求出AB的长度，然后利用勾股定理求出BE的长度，同理求得DF的长度，最后易求得AC的长度．
| 4 |
| 5 |
解答：解：作AE、CF⊥BC于点E、F，
在Rt△ABE中，
∵AE=2cm，sin∠B=
，
∴AB=AE÷sin∠B=2÷
=2.5，
∴BE=
=1.5，
同理可得，DF=BE=1.5cm，
则AC=4-1.5-1.5=1（cm）．
故答案为：1．
在Rt△ABE中，
∵AE=2cm，sin∠B=
| 4 |
| 5 |
∴AB=AE÷sin∠B=2÷
| 4 |
| 5 |
∴BE=
| 2．52-22 |
同理可得，DF=BE=1.5cm，
则AC=4-1.5-1.5=1（cm）．
故答案为：1．
点评：本题考查了等腰梯形的性质和解直角三角形，解答本题的关键是掌握等腰梯形同一底上的两个角相等的性质．
练习册系列答案
天天向上口算本系列答案
相关题目
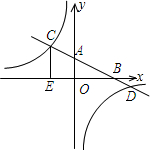已知：如图，在平面直角坐标系xOy中，直线AB分别与x、y轴交于点B、A，与反比例函数的图象分别交于点C、D，CE⊥x轴于点E，tan∠ABO=
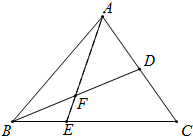如图，在△ABC中E是BC上的一点，EC=2EB，点D是AC的中点，AE、BD交于点F，AF=3FE．若△ABC的面积为18，给出下列命题：