题目内容
省教育厅2012年10月召开了“课内比教学,课外访万家”的视频会议.某中学七年级教师积极落实会议精神,制定了本学期下一阶段的家访计划.若每周访10个家庭,刚好按时完成计划任务;实际家访时,每周比原计划多访了2个家庭,总家访数比原计划也多了10个家庭,而时间比原计划提前一周.
(1)若设按原计划“家访”为x周,则可列方程为 ;若设实际的“家访”家庭数为y,则可列方程为
(2)选择(1)中的方法,求实际的“家访”家庭数.
(1)若设按原计划“家访”为x周,则可列方程为
(2)选择(1)中的方法,求实际的“家访”家庭数.
考点:一元一次方程的应用
专题:
分析:(1)设原计划家访时间为x周.实际每周家访个数:10+2=12(个).等量关系是:总家访数比原计划也多了10个家庭;
设实际的“家访”家庭数为y.等量关系是:时间比原计划提前一周;
(2)根据(1)中的方程进行解答即可.
设实际的“家访”家庭数为y.等量关系是:时间比原计划提前一周;
(2)根据(1)中的方程进行解答即可.
解答:解:(1)设原计划家访时间为x周,则(10+2)x-10x=10.
设实际的“家访”家庭数为y,则
-
=1.
故答案是:(10+2)x-10x=10;
-
=1;
(2)由(1)得,
-
=1.
解得 y=60.
答:实际的“家访”家庭数是60.
设实际的“家访”家庭数为y,则
| y |
| 10 |
| y |
| 10+2 |
故答案是:(10+2)x-10x=10;
| y |
| 10 |
| y |
| 10+2 |
(2)由(1)得,
| y |
| 10 |
| y |
| 10+2 |
解得 y=60.
答:实际的“家访”家庭数是60.
点评:本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
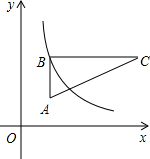 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4. 已知,如图,AD是△ABC的中线,且AD⊥BC.求证:AB=AC.
已知,如图,AD是△ABC的中线,且AD⊥BC.求证:AB=AC.