题目内容
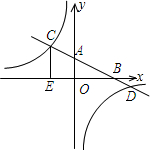 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=| 1 |
| 2 |
(1)求直线AB的解析式;
(2)求该反比例函数的解析式;
(3)连接OC,OD,求△COD的面积;
(4)在反比例函数图象上找一点P,使S△CPD=S△COD,求出P点坐标.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)先根据正切的定义计算出OA,则可得到A点坐标,然后利用待定系数法求直线AB的解析式;
(2)利用直线AB的解析式确定C点坐标,然后利用待定系数法求反比例函数解析式;
(3)先解方程组
得D点坐标为(4,-1),然后利用S△OCD=S△OAC+S△OAD进行计算;
(4)由于S△CPD=S△COD,而两三角形同底,所以先求出与直线AB平行且到AB的距离等于点O到AB的距离的两条直线y=-
x和y=-
x+2,然后分别把它们与反比例函数解析式组成方程组,再解方程组即可得到P点坐标.
(2)利用直线AB的解析式确定C点坐标,然后利用待定系数法求反比例函数解析式;
(3)先解方程组
|
(4)由于S△CPD=S△COD,而两三角形同底,所以先求出与直线AB平行且到AB的距离等于点O到AB的距离的两条直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)在Rt△ABO中,tan∠ABO=
=
,
而OB=2,则OA=1,
∴A点坐标为(0,1),
设直线AB的解析式为y=kx+b,
把A(0,1)、B(2,0)代入得
,
解得
.
∴直线AB的解析式为y=-
x+1;
(2)∵OE=2,
∴C点的横坐标为-2,
把x=-2代入y=-
x+1得y=-
×(-2)+1=2,
∴C点坐标为(-2,2),
设反比例函数解析式为y=
,
把C(-2,2)代入得m=-2×2=-4,
∴反比例函数解析式为y=-
;
(3)解方程组
得
或
,
S△OCD=S△OAC+S△OAD
=
×1×2+
×1×4
=3;
(4)过原点与直线AB平行的直线解析式为y=-
x,
解方程组
得
或
,
则P点坐标为(2
,-
)或(-2
,
);
把直线y=-
x向上平移2个单位得y=-
x+2,
解方程组
得
或
,
则P点坐标为(2+2
,1-
)或(2-2
,1+
).
| OA |
| OB |
| 1 |
| 2 |
而OB=2,则OA=1,
∴A点坐标为(0,1),
设直线AB的解析式为y=kx+b,
把A(0,1)、B(2,0)代入得
|
解得
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
(2)∵OE=2,
∴C点的横坐标为-2,
把x=-2代入y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴C点坐标为(-2,2),
设反比例函数解析式为y=
| m |
| x |

把C(-2,2)代入得m=-2×2=-4,
∴反比例函数解析式为y=-
| 4 |
| x |
(3)解方程组
|
|
|
S△OCD=S△OAC+S△OAD
=
| 1 |
| 2 |
| 1 |
| 2 |
=3;
(4)过原点与直线AB平行的直线解析式为y=-
| 1 |
| 2 |
解方程组
|
|
|
则P点坐标为(2
| 2 |
| 2 |
| 2 |
| 2 |
把直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
解方程组
|
|
|
则P点坐标为(2+2
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
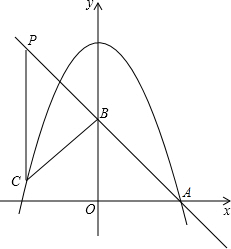 二次函数y=ax2+4的图象与x轴正半轴交于点A(2,0),点B(0,2)在y轴上,点P是直线AB上的一个动点,过点P作PC∥y轴交抛物线于点C,设点P的横坐标为m(m<2),求当△PBC是直角三角形时,直接写出m的值.
二次函数y=ax2+4的图象与x轴正半轴交于点A(2,0),点B(0,2)在y轴上,点P是直线AB上的一个动点,过点P作PC∥y轴交抛物线于点C,设点P的横坐标为m(m<2),求当△PBC是直角三角形时,直接写出m的值.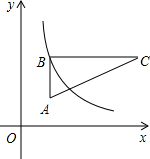 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC、BA分别平行于x轴、y轴,点C的坐标为(5,3),AB=2,BC=4. 如图,一轮船由西向东航行,从A点到B点航程为12千米,分别在A、B两处望小岛P,测得∠BAP=15°,∠DBP=30°.若小岛P周围6.8千米内有暗礁,问该船一直向东航行有无触礁的危险?
如图,一轮船由西向东航行,从A点到B点航程为12千米,分别在A、B两处望小岛P,测得∠BAP=15°,∠DBP=30°.若小岛P周围6.8千米内有暗礁,问该船一直向东航行有无触礁的危险? 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0). 如图,画出△ABC绕AC的中点M逆时针旋转90°的图形.
如图,画出△ABC绕AC的中点M逆时针旋转90°的图形.