题目内容
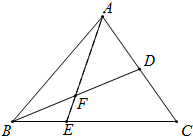 如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE.若△ABC的面积为18,给出下列命题:
如图,在△ABC中E是BC上的一点,EC=2EB,点D是AC的中点,AE、BD交于点F,AF=3FE.若△ABC的面积为18,给出下列命题:①△ABE的面积为6;
②△ABF的面积和四边形DFEC的面积相等;
③点F是BD的中点;
④四边形DFEC的面积为
| 15 |
| 2 |
其中,正确的结论有
考点:三角形的面积
专题:
分析:①根据等高的三角形面积比等于底边比即可求解;
②先分别得到△ABE的面积和四边形DBC的面积与△ABC的面积之间的关系,依此即可求解;
③过D点作DG∥BC,通过三角形中位线定理和全等三角形的判定和性质即可求解;
④用18-△ABF的面积-△ADF的面积,列式计算即可求解.
②先分别得到△ABE的面积和四边形DBC的面积与△ABC的面积之间的关系,依此即可求解;
③过D点作DG∥BC,通过三角形中位线定理和全等三角形的判定和性质即可求解;
④用18-△ABF的面积-△ADF的面积,列式计算即可求解.
解答:解:①∵△ABC的面积为18,EC=2EB,
∴△ABE的面积=18×
=6,故①正确;
 ②∵EC=2EB,点D是AC的中点,
②∵EC=2EB,点D是AC的中点,
∴△ABE的面积≠△BCD的面积,
∴△ABF的面积和四边形DFEC的面积不相等,故②错误;
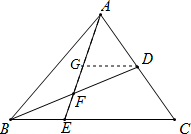
③过D点作DG∥BC,
∵点D是AC的中点,
∴DG=
EC,
∵EC=2EB,
∴DG=BE,
∵DG∥BC,
∴∠DGF=∠BEF,∠GDF=∠EBF,
在△DGF与△BEF中,
,
∴△DGF≌△BEF(ASA),
∴DF=BF,
∴点F是BD的中点,故③正确;
④四边形DFEC的面积=18-18×
-18×
×
=18-6-
=
,故④正确.
故正确的结论有①③④.
故答案为:①③④.
∴△ABE的面积=18×
| 1 |
| 3 |
 ②∵EC=2EB,点D是AC的中点,
②∵EC=2EB,点D是AC的中点,∴△ABE的面积≠△BCD的面积,
∴△ABF的面积和四边形DFEC的面积不相等,故②错误;
③过D点作DG∥BC,
∵点D是AC的中点,
∴DG=
| 1 |
| 2 |
∵EC=2EB,
∴DG=BE,
∵DG∥BC,
∴∠DGF=∠BEF,∠GDF=∠EBF,
在△DGF与△BEF中,
|
∴△DGF≌△BEF(ASA),
∴DF=BF,
∴点F是BD的中点,故③正确;
④四边形DFEC的面积=18-18×
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=18-6-
| 9 |
| 2 |
=
| 15 |
| 2 |
故正确的结论有①③④.
故答案为:①③④.
点评:本题考查三角形的面积,关键知道当高相等时,面积等于底边的比,根据此可求出三角形的面积,然后求出差.

练习册系列答案
相关题目
如果单项式-2xa+1y3与
x2yb是同类项,那么a,b的值分别为( )
| 1 |
| 2 |
| A、a=1,b=3 |
| B、a=1,b=2 |
| C、a=2,b=3 |
| D、a=2,b=2 |