题目内容
4. 如图,AB=AC,BD=CD.
如图,AB=AC,BD=CD.(1)求证:∠B=∠C;
(2)若∠BAC=120°,∠BDC=80°,求∠B的度数.
分析 (1)连接AD,证明△ABD与△ACD全等,即可求解;
(2)根据全等三角形的性质得出∠C=∠B,再利用四边形的内角和解答即可.
解答 证明:(1)连接AD,如图:
在△ABD与△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{BD=CD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD(SSS),
∴∠B=∠C;
(2)∵△ABD≌△ACD,
∴∠B=∠C,
在四边形ABCD中,∠B=$\frac{1}{2}(360°-120°-80°)=80°$.
点评 此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质和四边形内角和定理,关键是根据题意作出辅助线.

练习册系列答案
相关题目
14.倡导“节能减排”,鼓励居民节约用电,2012年7月起,湖北省开始试行城乡居民用户阶梯电价制度,方案如下:
如:小明家3月份用电量为500度,则应付费:180×0.573+(400-180)×0.623+(500-400)×0.873=327.5元
(1)若小华家4月用电量为100度,则应付电费57.3元,5月用电量为210度,则应付电费121.83元,6月用电量450度,则应付电费283.85元?
(2)若小华家7月份的用电量为x度,请用x表示电费;
(3)若小华家9月份已付电费177.9元,请你求出小华家9月的用电量.
(4)若小华家某月的电费为a元,则小华家该月用电量属于第几档.
| 月用电量类型 | 第一档电量 | 第二档电量 | 第三档电量 |
| 月用电量 | 不超过180度 | 超过180度,不超过400度 | 超过400度 |
| 电费标准 | 用电量180度及以下,每度电价格为0.573元, 超过180度而不超过400度的部分,每度电价格为0.623元; 超过400度的部分,每度电价格为0.873元. | ||
(1)若小华家4月用电量为100度,则应付电费57.3元,5月用电量为210度,则应付电费121.83元,6月用电量450度,则应付电费283.85元?
(2)若小华家7月份的用电量为x度,请用x表示电费;
(3)若小华家9月份已付电费177.9元,请你求出小华家9月的用电量.
(4)若小华家某月的电费为a元,则小华家该月用电量属于第几档.
 如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y.
如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B,C不重合),且DQ⊥AP,垂足为Q.设AP=x.DQ=y.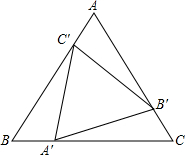 已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形. 如图,在直角梯形ABCD中,∠D=∠C=90°.若∠DAB的平分线AE交CD于E,连接BE,且BE恰好平分∠ABC.求证:AB=BC+AD.
如图,在直角梯形ABCD中,∠D=∠C=90°.若∠DAB的平分线AE交CD于E,连接BE,且BE恰好平分∠ABC.求证:AB=BC+AD.