题目内容
14.设a、b、c是实数,若a+b+c=2$\sqrt{a+1}$+4$\sqrt{b+1}$+6$\sqrt{c-2}$-14,则$\frac{a+c}{b+2a}$=$\frac{11}{3}$.分析 先移项,再利用配方法得到a+1-2$\sqrt{a+1}$+1+b+1-4$\sqrt{b+1}$+4+c-2-6$\sqrt{c-2}$+9=0,即有($\sqrt{a+1}$-1)2+($\sqrt{b+1}$-2)2+($\sqrt{c-2}$-3)2=0,然后根据非负数的性质解得a=0,b=3,c=11,最后代入求得数值.
解答 解:∵a+b+c=2$\sqrt{a+1}$+4$\sqrt{b+1}$+6$\sqrt{c-2}$-14,
∴a+1-2$\sqrt{a+1}$+1+b+1-4$\sqrt{b+1}$+4+c-2-6$\sqrt{c-2}$+9=0,
∴($\sqrt{a+1}$-1)2+($\sqrt{b+1}$-2)2+($\sqrt{c-2}$-3)2=0,
∴$\sqrt{a+1}$-1=0,$\sqrt{b+1}$-2=0,$\sqrt{c-2}$-3=0,
∴a=0,b=3,c=11,
则$\frac{a+c}{b+2a}$=$\frac{11}{3}$.
故答案为:$\frac{11}{3}$.
点评 本题考查了配方法的应用,非负数的性质,主要利用完全平方公式a2±2ab+b2=(a±b)2分组分解解决问题.

练习册系列答案
相关题目
9.下列判断中,正确的是( )
| A. | 平方等于它本身的有理数是1,或-1,或0 | |
| B. | 倒数等于它本身的有理数是1,或-1,或0 | |
| C. | 平方等于9的有理数是3和-3 | |
| D. | $\frac{355}{113}$是圆周率的近似值,因此$\frac{355}{113}$是无理数 |
19.一个水分子的质量大约为3×10-26kg,一位学生饮用了180g水,他大约喝下去的水分子个数约为( )
| A. | 6×1023 | B. | 180×6×1023 | C. | 18×6×1023 | D. | 6×1024 |
 如图,AB=AC,BD=CD.
如图,AB=AC,BD=CD.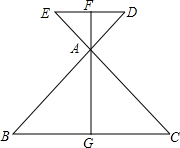 如图所示,BD与CE相交于点A,且AB=AC,AD=AE,△ABC的中线AG的反向延长线交DE于点F,则AF与DE垂直吗?用“三线合一”的方法说明理由.
如图所示,BD与CE相交于点A,且AB=AC,AD=AE,△ABC的中线AG的反向延长线交DE于点F,则AF与DE垂直吗?用“三线合一”的方法说明理由. 如图,在Rt△ABC的中,∠C=90°,AD是∠BAC的角平分线,且∠DAC=2∠B,求∠BAC,∠B,∠ADC的度数.
如图,在Rt△ABC的中,∠C=90°,AD是∠BAC的角平分线,且∠DAC=2∠B,求∠BAC,∠B,∠ADC的度数.