题目内容
14.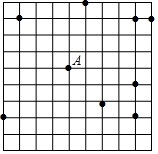 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.
分析 先根据勾股定理计算点A与其它格点的距离,根据点和圆的位置关系确定半径的取值.
解答 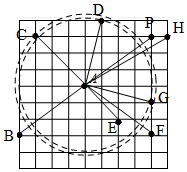 解:分别连接A与其它各格点,
解:分别连接A与其它各格点,
由勾股定理得:AB=$\sqrt{{4}^{2}+{4}^{2}}$=$\sqrt{32}$=4$\sqrt{2}$,
AC=$\sqrt{{3}^{2}+{3}^{2}}$=$\sqrt{18}$=3$\sqrt{2}$,
AD=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
AE=$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,
AF=$\sqrt{{4}^{2}+{3}^{2}}$=5,
AG=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
AH=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
AP=$\sqrt{{3}^{2}+{4}^{2}}$=5,
当r=3$\sqrt{2}$时,有三个点在圆内:D、E、G,
当r=$\sqrt{17}$时,点E在圆内,点D和G在圆上,
则r的取值范围为:$\sqrt{17}$<r≤3$\sqrt{2}$.
故答案为:$\sqrt{17}$<r≤3$\sqrt{2}$.
点评 本题考查了点和圆的位置关系,点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.当点与圆心的距离小于半径时,该点在圆内.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.下列图形中,轴对称图形的个数为( )

| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.下列运算正确的是( )
| A. | a-1÷a3=a2 | B. | ($\frac{1}{3}$)0=0 | C. | 3-2=$\frac{1}{9}$ | D. | (a2)3=a5 |
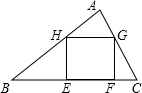 如图,在Rt△ABC中,∠A=90°,正方形EFGH的四个顶点在三角形的边上,已知BE=6,FC=2,则正方形EFGH的边长等于2$\sqrt{3}$.
如图,在Rt△ABC中,∠A=90°,正方形EFGH的四个顶点在三角形的边上,已知BE=6,FC=2,则正方形EFGH的边长等于2$\sqrt{3}$.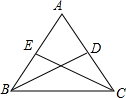 如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)
如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.(请填空)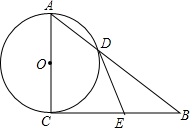 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.