题目内容
9.已知二次函数y=x2+mx+n(m,n为常数).(1)若m=-2,n=-4,求二次函数的最小值;
(2)若n=3,该二次函数的图象与直线y=1只有一个公共点,求m的值;
(3)若n=m2,且3m+4<0,当x满足m≤x≤m+2时,y有最小值13,求此二次函数的解析式.
分析 (1)将m=-2,n=-4代入二次函数y=x2+mx+n,易得二次函数的最值;
(2)将n=3代入y=x2+mx+n,令y=1可得x2+mx+3=1,利用根的判别式,可得△=m2-8=0,解得m;
(3)根据已知3m+4<0,可得m的取值范围,因为n=m2,可得抛物线y=x2+mx+m2的对称轴为x=$-\frac{m}{2}$,可得对称轴的取值范围,根据该二次函数的增减性可得当x=m+2,y有最小值为13,易得(m+2)2+m(m+2)+m2=13,解得m,根据m的取值范围确定m的值.
解答 解:(1)当m=-2,n=-4时,y=x2-2x-4=(x-1)2-5
∴当x=1时,y最小值=-5;
(2)当n=3时,y=x2+mx+3,
令y=1,则x2+mx+3=1,
由题意知,x2+mx+3=1有两个相等的实数根,
则△=m2-8=0,
∴m=$±2\sqrt{2}$;
(3)由3m+4<0,可知m$<-\frac{4}{3}$,
∴m≤x≤m+2$<\frac{2}{3}$,
抛物线y=x2+mx+m2的对称轴为x=$-\frac{m}{2}$,
∵m$<-\frac{4}{3}$,
∴$-\frac{m}{2}$$>\frac{2}{3}$,
∴对称轴为x=$-\frac{m}{2}$$>\frac{2}{3}$,
∴在m≤x≤m+2时,y随x的增大而减小,
∴当x=m+2,y有最小值为13,
∴(m+2)2+m(m+2)+m2=13,
即m2+2m-3=0,
解得m=1或m=-3,而m$<-\frac{4}{3}$,
∴m=-3,
此时,y=x2-3x+9.
点评 本题主要考查了二次函数的性质,结合已知条件确定m的值是解答此题的关键.

练习册系列答案
相关题目
19.-3的相反数是( )
| A. | -$\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | -3 |
17.一只不透明的袋子中装有7个红球、3个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到红球的概率为( )
| A. | $\frac{7}{10}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{7}$ |
1.已知关于x的分式方程$\frac{a+2}{x+1}$=1的解是非正数,则a的取值范围是( )
| A. | a≤-1 | B. | a≤1且a≠-2 | C. | a≤-1且a≠-2 | D. | a≤1 |
18.已知方程x2k-1+3=0是关于x的一元一次方程,则k的值等于( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
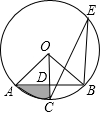 如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)
如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)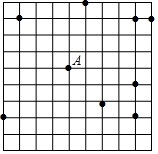 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为$\sqrt{17}<r≤3\sqrt{2}$.