题目内容
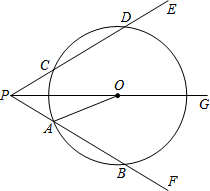 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.(1)求证:AP=AO;
(2)若弦AB=12,求tan∠OPB的值;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为
考点:圆的综合题,全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理,菱形的判定与性质,等腰梯形的判定,垂径定理,圆内接四边形的性质
专题:综合题
分析:(1)由PG平分∠EPF可得∠CPO=∠APO,由AO∥PD可得∠CPO=∠AOP,从而有∠APO=∠AOP,则有AP=AO.
(2)过点O作OH⊥AB于H,如图2.根据垂径定理可得AH=BH=6,从而可求出PH,在Rt△AHO中,运用勾股定理可求出OH,然后运用锐角三角函数的定义就可解决问题.
(3))①过点O作OH⊥AB于H,过点O作OQ⊥CD于Q,连接OC,如图3.易证△PQO≌△PHO,则有PQ=PH,OQ=OH,从而可证到Rt△OQC≌Rt△OHA(HL),则有QC=HA,从而可证到PC=PA=OA=OC,因而四边形PAOC是菱形.②连接OC、OB,如图4.由四边形PAOC是菱形可得OC∥PA,易证PC=OB,故四边形PCOB是等腰梯形.③连接OC、OD,如图5.同理可得梯形PAOD是等腰梯形.④连接OC、AC、BD,如图6.由四边形PAOC是菱形可得PA=PC,则有∠PAC=∠PCA.根据圆内接四边形的性质可得∠PAC=∠PDB,∠PCA=∠PBD,从而有∠PAC=∠PDB=∠PCA=∠PBD,则有PD=PB,AC∥BD,易证CD=AB,故四边形ABDC是等腰梯形.
(2)过点O作OH⊥AB于H,如图2.根据垂径定理可得AH=BH=6,从而可求出PH,在Rt△AHO中,运用勾股定理可求出OH,然后运用锐角三角函数的定义就可解决问题.
(3))①过点O作OH⊥AB于H,过点O作OQ⊥CD于Q,连接OC,如图3.易证△PQO≌△PHO,则有PQ=PH,OQ=OH,从而可证到Rt△OQC≌Rt△OHA(HL),则有QC=HA,从而可证到PC=PA=OA=OC,因而四边形PAOC是菱形.②连接OC、OB,如图4.由四边形PAOC是菱形可得OC∥PA,易证PC=OB,故四边形PCOB是等腰梯形.③连接OC、OD,如图5.同理可得梯形PAOD是等腰梯形.④连接OC、AC、BD,如图6.由四边形PAOC是菱形可得PA=PC,则有∠PAC=∠PCA.根据圆内接四边形的性质可得∠PAC=∠PDB,∠PCA=∠PBD,从而有∠PAC=∠PDB=∠PCA=∠PBD,则有PD=PB,AC∥BD,易证CD=AB,故四边形ABDC是等腰梯形.
解答:(1)证明:如图1,

∵PG平分∠EPF,
∴∠CPO=∠APO.
∵AO∥PD,
∴∠CPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO.
(2)解:过点O作OH⊥AB于H,如图2.

根据垂径定理可得AH=BH=
AB=6,
∴PH=PA+AH=AO+AH=10+6=16.
在Rt△AHO中,
OH=
=
=8,
∴tan∠OPB=
=
=
.
∴tan∠OPB的值为
.
(3)解:①过点O作OH⊥AB于H,过点O作OQ⊥CD于Q,连接OC,如图3.

在△PQO和△PHO中,
,
∴△PQO≌△PHO(AAS),
∴PQ=PH,OQ=OH.
在Rt△OQC和Rt△OHA中,
,
∴Rt△OQC≌Rt△OHA(HL),
∴QC=HA,
∴PC=PA,
∴PC=PA=OA=OC,
∴四边形PAOC是菱形.
②连接OC、OB,如图4.

∵四边形PAOC是菱形,∴OC∥PA.
∵PC∥OA,∴PC与OB不平行,
∴四边形PCOB是梯形.
∵PC=OA=OB,
∴梯形PCOB是等腰梯形.
③连接OC、OD,如图5.

∵四边形PAOC是菱形,
∴PA∥OC,
∴PA与OD不平行.
∵OA∥PD,
∴四边形PAOD是梯形.
∵PA=OA=OD,
∴梯形PAOD是等腰梯形.
④连接OC、AC、BD,如图6.

∵四边形PAOC是菱形,
∴PA=PC,
∴∠PAC=∠PCA.
根据圆内接四边形的性质可得:∠PAC=∠PDB,∠PCA=∠PBD,
∴∠PAC=∠PDB=∠PCA=∠PBD,
∴PD=PB,AC∥BD,
∵CD与AB不平行,
∴四边形ABDC是梯形,
∵CD=PD-PC=PB-PA=AB,
∴梯形ABDC是等腰梯形.
故答案为:P、A、O、C;P、A、O、D;P、B、O、C;A、B、D、C.

∵PG平分∠EPF,
∴∠CPO=∠APO.
∵AO∥PD,
∴∠CPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO.
(2)解:过点O作OH⊥AB于H,如图2.

根据垂径定理可得AH=BH=
| 1 |
| 2 |
∴PH=PA+AH=AO+AH=10+6=16.
在Rt△AHO中,
OH=
| OA2-AH2 |
| 100-36 |
∴tan∠OPB=
| OH |
| PH |
| 8 |
| 16 |
| 1 |
| 2 |
∴tan∠OPB的值为
| 1 |
| 2 |
(3)解:①过点O作OH⊥AB于H,过点O作OQ⊥CD于Q,连接OC,如图3.

在△PQO和△PHO中,
|
∴△PQO≌△PHO(AAS),
∴PQ=PH,OQ=OH.
在Rt△OQC和Rt△OHA中,
|
∴Rt△OQC≌Rt△OHA(HL),
∴QC=HA,
∴PC=PA,
∴PC=PA=OA=OC,
∴四边形PAOC是菱形.
②连接OC、OB,如图4.

∵四边形PAOC是菱形,∴OC∥PA.
∵PC∥OA,∴PC与OB不平行,
∴四边形PCOB是梯形.
∵PC=OA=OB,
∴梯形PCOB是等腰梯形.
③连接OC、OD,如图5.

∵四边形PAOC是菱形,
∴PA∥OC,
∴PA与OD不平行.
∵OA∥PD,
∴四边形PAOD是梯形.
∵PA=OA=OD,
∴梯形PAOD是等腰梯形.
④连接OC、AC、BD,如图6.

∵四边形PAOC是菱形,
∴PA=PC,
∴∠PAC=∠PCA.
根据圆内接四边形的性质可得:∠PAC=∠PDB,∠PCA=∠PBD,
∴∠PAC=∠PDB=∠PCA=∠PBD,
∴PD=PB,AC∥BD,
∵CD与AB不平行,
∴四边形ABDC是梯形,
∵CD=PD-PC=PB-PA=AB,
∴梯形ABDC是等腰梯形.
故答案为:P、A、O、C;P、A、O、D;P、B、O、C;A、B、D、C.
点评:本题考查了垂径定理、圆内接四边形的性质、全等三角形的判定与性质、菱形的判定与性质、等腰三角形的判定与性质、等腰梯形的判定、勾股定理、锐角三角函数的定义、平行线的性质、角平分线的定义等知识,综合性比较强.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
已知a、b为有理数,则多项式a2+b2-2a-6b+12的值为( )
| A、正数 | B、零 | C、负数 | D、非负数 |
 已知△ABC,
已知△ABC, 如图为6个边长相等的正方形的组合图形,则∠1+∠3=
如图为6个边长相等的正方形的组合图形,则∠1+∠3=