题目内容
设A(-1,y1),B(0,y2),C(1,y3)是抛物线y=(x+1)2+a上的三点,则y1、y2、y3的大小关系为 .(用“>”号连接)
考点:二次函数图象与系数的关系
专题:
分析:先配方得到抛物线的对称轴为直线x=-1,根据二次函数的性质,通过三点与对称轴距离的远近来比较函数值的大小.
解答:解:∵y=(x+1)2+a,
∴抛物线的对称轴为直线x=-1,
∵抛物线开口向下,而点A(-1,y1)在对称轴上,B(0,y2)到对称轴的距离比C(1,y3)近,
∴y1>y2>y3.
故答案为:y1>y2>y3.
∴抛物线的对称轴为直线x=-1,
∵抛物线开口向下,而点A(-1,y1)在对称轴上,B(0,y2)到对称轴的距离比C(1,y3)近,
∴y1>y2>y3.
故答案为:y1>y2>y3.
点评:本题考查了二次函数图象与系数的关系.此题需要掌握二次函数图象的增减性.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
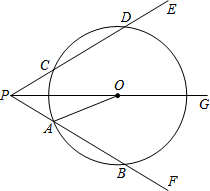 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.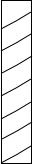 如图,有一根高为2m的圆柱形木材,它的底面周长为0.3m.为了营造喜庆的气氛,小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈,一直缠到起点的正上方为止.小颖至少要准备多长的一根彩带?
如图,有一根高为2m的圆柱形木材,它的底面周长为0.3m.为了营造喜庆的气氛,小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈,一直缠到起点的正上方为止.小颖至少要准备多长的一根彩带?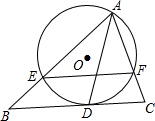 如图,直线BC与半径为2的⊙O相切于点D,A是⊙O上一点,AB交⊙O于点E,AC交⊙O于点F,BC∥EF.
如图,直线BC与半径为2的⊙O相切于点D,A是⊙O上一点,AB交⊙O于点E,AC交⊙O于点F,BC∥EF.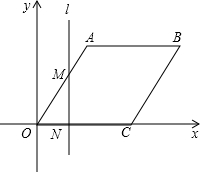 如图,在平面直角坐标系中,OA∥CB,AB∥OC,∠AOC=60°,OC=OA=4;
如图,在平面直角坐标系中,OA∥CB,AB∥OC,∠AOC=60°,OC=OA=4;